利用主成分分析（PCA）简化数据

一．PCA基础

线性映射（或线性变换），简单的来说就是将高维空间数据投影到低维空间上，那么在数据分析上，我们是将数据的主成分（包含信息量大的维度）保留下来，忽略掉对数据描述不重要的成分。即将主成分维度组成的向量空间作为低维空间，将高维数据投影到这个空间上就完成了降维的工作。

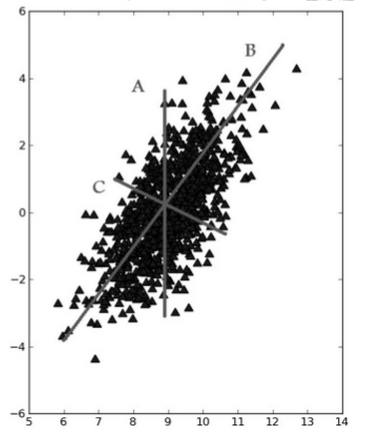
在 PCA中,数据从原来的坐标系转换到了新的坐标系,新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复,重复次数为原始数据中特征的数目。我们会发现,大部分方差都包含在最前面的几个新坐标轴中。因此,我们可以忽略余下的坐标轴,即对数据进行了降维处理。

工作原理：

①找出第一个主成分的方向，也就是数据 方差最大 的方向。

②找出第二个主成分的方向，也就是数据 方差次大 的方向，并且该方向与第一个主成分方向正交(果是二维空间就叫垂直)。

③通过这种方式计算出所有的主成分方向。

④通过数据集的协方差矩阵及其特征值分析，我们就可以得到这些主成分的值。

⑤一旦得到了协方差矩阵的特征值和特征向量，我们就可以保留最大的 N 个特征。这些特征向量也给出了 N 个最重要特征的真实结构，我们就可以通过将数据乘上这 N 个特征向量 从而将它转换到新的空间上。

二．PCA在NumPy中的实现

def loadDataSet(fileName, delim='\t') :
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    dataArr = [map(float, line) for line in stringArr]
    return mat(dataArr)

# dataMat: 用于进行PCA操作的数据集
# topNfeat: 可选参数，即应用的N个特征。
# 若不指定topNfeat的值，那么函数就会返回前9999999个特征，或者原始数据中的全部特征
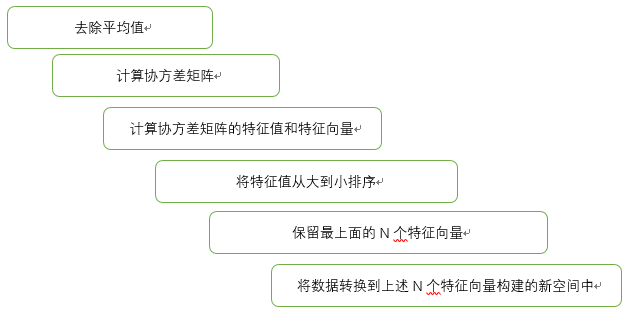
def pca(dataMat, topNfeat=9999999) :
    # 计算平均值
    meanVals = mean(dataMat, axis=0)
    # 减去原始数据的平均值
    meanRemoved = dataMat - meanVals
    # 计算协方差矩阵及其特征值
    covMat = cov(meanRemoved, rowvar=0)
    eigVals, eigVects = linalg.eig(mat(covMat))
    # 利用argsort()函数对特征值进行从小到大的排序，根据特征值排序结果的逆序就可以得到
    # topNfeat个最大的特征向量
    eigValInd = argsort(eigVals)
    eigValInd = eigValInd[:-(topNfeat+1):-1]
    # 这些特征向量将构成后面对数据进行转换的矩阵，该矩阵则利用N个特征将原始数据转换到新空间中
    redEigVects = eigVects[:, eigValInd]
    lowDDataMat = meanRemoved * redEigVects
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat

注意：与python2有点不同，python3要加list

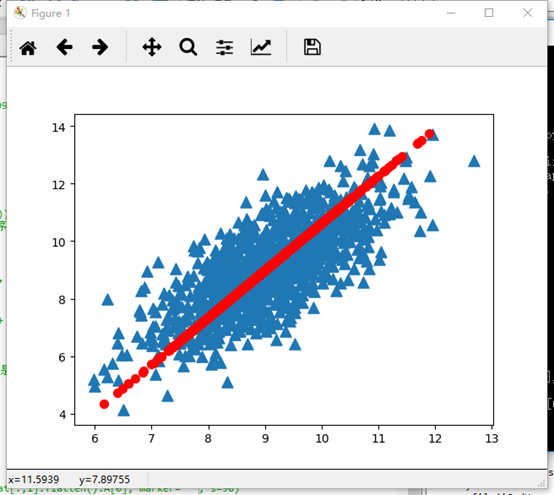
>>> dataMat = pca.loadDataSet('testSet.txt')
>>> lowDMat, reconMat = pca.pca(dataMat, 1)
>>> import numpy
>>> numpy.shape(lowDMat)
(1000, 1)
>>> import matplotlib
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.scatter(dataMat[:,0].flatten().A[0], dataMat[:,1].flatten().A[0], marker='^', s=90)
<matplotlib.collections.PathCollection object at 0x000002449DCFA2B0>
>>> ax.scatter(reconMat[:,0].flatten().A[0], reconMat[:,1].flatten().A[0], marker='o', s=50, c='red')
<matplotlib.collections.PathCollection object at 0x000002449DCFABE0>
>>> plt.show()

得到如图

三．利用PCA对半导体制造数据降维

def replaceNaNWithMean():
    #解析数据
    datMat=loadDataSet('secom.data',' ')
   #获取特征维度
    numFeat=shape(datMat)[1]
    #遍历数据集每一个维度
    for i in range(numFeat):
        #利用该维度所有非NaN特征求取均值
        meanVal=mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i])
        #将该维度中所有NaN特征全部用均值替换
        datMat[nonzero(isnan(datMat[:,i].A))[0],i]=meanVal
    return datMat

dataMat=replaceNaNWithMean()
meanVals=mean(dataMat,axis=0)
meanRemoved=dataMat-meanVals
conMat=cov(meanRemoved,rowvar=0)
eigVals,eigVects=linalg.eig(mat(covMat))
eigVects

结果出现错误

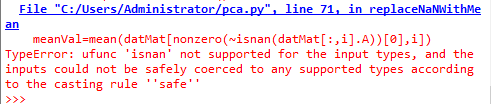
错误有待解决，也希望知道原因的小伙伴能告知一下，非常感谢