Machine Learning（CF940F+带修改莫队）

题目链接：http://codeforces.com/problemset/problem/940/F

题目：

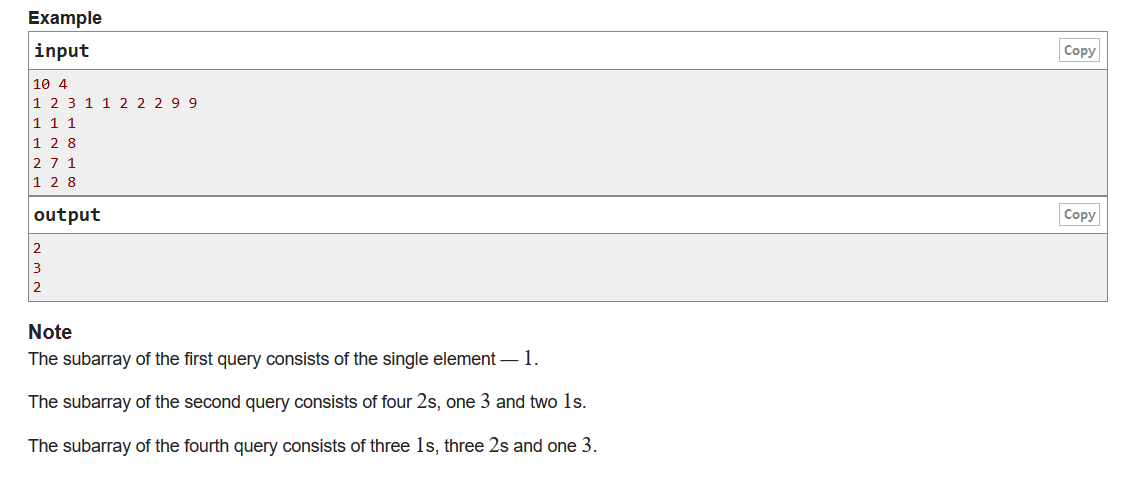
题意：求次数的mex，mex的含义为某个集合（如{1，2，4，5}）第一个为出现的非负数（3），注意是次数，而不是某个元素的mex。

思路：这一题数据太大，所以我们首先得进行一次离散化。用一个num2来记录每个次数出现次数，num1来记录次数出现次数，最后用一个for循环来求出mex。

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long ll;
 typedef unsigned long long ull;

 #define bug printf("*********\n");
 #define FIN freopen("in.txt", "r", stdin);
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = 1e9 + ;
 const int maxn = 1e5 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const ll INF = 0x3f3f3f3f3f3f3f3f;

 inline int read() {//读入挂
     int ret = , c, f = ;
     for(c = getchar(); !(isdigit(c) || c == '-'); c = getchar());
     if(c == '-') f = -, c = getchar();
     for(; isdigit(c); c = getchar()) ret = ret *  + c - '';
     if(f < ) ret = -ret;
     return ret;
 }

 int n, q, block, idq, idc, x, y;
 int a[maxn], num1[ * maxn], num2[ * maxn];
 vector<int> v;

 struct query {
     int l, r, id, t, ans;
     bool operator < (const query& x) const {
         if((l - ) / block != (x.l - ) / block) {
             return l < x.l;
         }
         if((r - ) / block != (x.r - ) / block) {
             return r < x.r;
         }
         return t < x.t;
     }
 }ask[maxn];

 struct modify {
     int p, pre, val;
 }myf[maxn];

 int get_id(int x) {
     return lower_bound(v.begin(), v.end(), x) - v.begin() + ;
 }

 void add(int x) {
     num1[num2[x]]--;
     num2[x]++;
     num1[num2[x]]++;
 }

 void del(int x) {
     num1[num2[x]]--;
     num2[x]--;
     num1[num2[x]]++;
 }

 int main() {
     //FIN;
     num1[] = 1e8;
     n = read();
     q = read();
     block = ;
     for(int i = ; i <= n; i++) {
         a[i] = read();
         v.push_back(a[i]);
     }
     int nw = ;
     for(int i = ; i <= q; i++) {
         int op;
         op = read();
         if(op == ) {
             x = read();
             y = read();
             idq++;
             ask[idq].l = x, ask[idq].r = y;
             ask[idq].id = idq;
             ask[idq].t = nw;
         } else {
             x = read();
             y = read();
             idc++;
             nw++;
             myf[idc].p = x;
             myf[idc].pre = a[x];
             myf[idc].val = y;
             a[x] = y;
             v.push_back(y);
         }
     }
     sort(v.begin(), v.end());
     v.erase(unique(v.begin(), v.end()), v.end());
     sort(ask + , ask + idq + );
     for(int i = ; i <= n; i++) {
         a[i] = get_id(a[i]);
     }
     for(int i = ; i <= idc; i++) {
         myf[i].pre = get_id(myf[i].pre);
         myf[i].val = get_id(myf[i].val);
     }
     int tmp = nw, r = , l = ;
     for(int i = ; i <= idq; i++) {
         int res = ;
         while(r > ask[i].r) {
             del(a[r--]);
         }
         while(r < ask[i].r) {
             add(a[++r]);
         }
         while(l > ask[i].l) {
             add(a[--l]);
         }
         while(l < ask[i].l) {
             del(a[l++]);
         }
         while(tmp < ask[i].t) {
             tmp++;
             if(myf[tmp].p >= l && myf[tmp].p <= r) {
                 del(myf[tmp].pre);
                 add(myf[tmp].val);
             }
             a[myf[tmp].p] = myf[tmp].val;
         }
         while(tmp > ask[i].t) {
             if(myf[tmp].p >= l && myf[tmp].p <= r) {
                 del(myf[tmp].val);
                 add(myf[tmp].pre);
             }
             a[myf[tmp].p] = myf[tmp].pre;
             tmp--;
         }
         while(num1[res] > ) res++;
         ask[ask[i].id].ans = res;
     }
     for(int i = ; i <= idq; i++) {
         printf("%d\n", ask[i].ans);
     }
     return ;
 }