【BZOJ3453】XLkxc [拉格朗日插值法]

XLkxc

Time Limit: 20 Sec  Memory Limit: 128 MB
[Submit][Status][Discuss]

Description

　　给定 k,a,n,d,p
　　f(i)=1^k+2^k+3^k+......+i^k
　　g(x)=f(1)+f(2)+f(3)+....+f(x)
　　求(g(a)+g(a+d)+g(a+2d)+......+g(a+nd))mod p

Input

　　第一行数据组数，(保证小于6)
　　以下每行四个整数 k,a,n,d

Output

　　每行一个结果。

Sample Input

　　5
　　1 1 1 1
　　1 1 1 1
　　1 1 1 1
　　1 1 1 1
　　1 1 1 1

Sample Output

　　5
　　5
　　5
　　5
　　5

HINT

　　1<=k<=123
　　0<=a,n,d<=123456789
　　p==1234567891

Main idea

　　给定k,a,n,d，求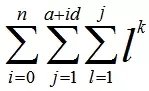

Solution

　　我们可以令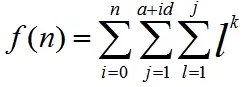

　　然后推一波式子，再令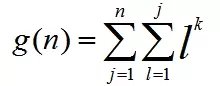

　　那么显然有

　　然后我们通过若干次差分，发现g在差分k+3次时全为0，那么g就是一个k+2次多项式；f在差分k+5次时全为0，那么f就是一个k+4次多项式。

　　我们通过拉格朗日插值法插g，得到k+5个f的值，然后再插值f就可以得到答案了。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64;
 const int ONE=;
 const s64 MOD=;

 int T;
 int k,a,n,d;
 int g[ONE],f[ONE];
 int inv[ONE],U[ONE],Jc[ONE];
 int pre[ONE],suc[ONE];

 int get()
 {
         int res=,Q=;  char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 int Quickpow(int a,int b)
 {
         int res=;
         while(b)
         {
             if(b&) res=(s64)res*a%MOD;
             a=(s64)a*a%MOD;
             b>>=;
         }
         return res;
 }

 int P(int k,int i)
 {
         if((k-i)&) return -+MOD;
         return ;
 }

 namespace First
 {
         void Deal_jc(int k)
         {
             Jc[]=;
             for(int i=;i<=k;i++) Jc[i]=(s64)Jc[i-]*i%MOD;
         }

         void Deal_inv(int k)
         {
             inv[]=;    inv[k]=Quickpow(Jc[k],MOD-);
             for(int i=k-;i>=;i--) inv[i]=(s64)inv[i+]*(i+)%MOD;
         }
 }

 int Final(int f[],int n,int k)
 {
         pre[]=;    for(int i=;i<=k;i++) pre[i]=(s64)pre[i-] * (n-i+MOD) % MOD;
         suc[]=;    for(int i=;i<=k;i++) suc[i]=(s64)suc[i-] * (s64)(n-k+i-+MOD) % MOD;

         s64 Ans=;
         for(int i=;i<=k;i++)
         {
             int Up=   (s64) pre[i-]*suc[k-i] % MOD * f[i] % MOD;
             int Down= (s64) inv[i-]*inv[k-i] % MOD;

             Ans=(s64)(Ans + (s64) Up*Down % MOD * P (k,i) %MOD) % MOD;
         }

         return Ans;
 }

 int main()
 {
         First::Deal_jc();    First::Deal_inv();
         T=get();
         while(T--)
         {
             k=get();    a=get();    n=get();    d=get();

             for(int i=;i<=k+;i++) g[i]=Quickpow(i,k);
             for(int i=;i<=k+;i++) g[i]=((s64)g[i-]+g[i])%MOD;
             for(int i=;i<=k+;i++) g[i]=((s64)g[i-]+g[i])%MOD;
             for(int i=;i<=k+;i++)
             f[i]=((s64)f[i-]+Final(g,(a+(s64)i*d)%MOD,k+)) % MOD;

             printf("%d\n",Final(f,n,k+)%MOD);
         }
 }