Manacher算法总结

部分图片转自：http://www.cnblogs.com/grandyang/p/4475985.html

manacher算法（民间称马拉车算法233）是用来找字符串中的最长回文子串的，先来说一下什么是回文串，像这样“abcba”这样一个字符串找到一个中间位置，然后分别向他的左边和右边相等的距离位置的字符是相同的，那么这个字符串就称为回文串，“abcba”这个字符串的len为5是奇数，我们可以找到一个中间字符，然后进行搜索也可以找出来（当然时间复杂度是比较高的），但是当我们遇到一个长度为偶数的字符串时该怎么找中间字符呢，像这样“abccba”，下面我们引入Manacher算法，这是一个可以将长度为奇数或偶数的字符串一起考虑的神奇算法

Manacher算法可以将长度为奇数和偶数的回文串一起考虑：在原字符串的相邻字符串之间插入一个分隔符，字符串的首尾也要分别添加，注意分隔符必须是原字符串中没有出现过的

原字符串s

a

b

a

b

c

转换后字符串str

#

a

#

b

#

a

#

b

#

c

#

一、Len数组的简单介绍

Manacher算法中用到一个非常重要的辅助数组Len[i]表示以str[i]为中心的最长回文子串的最右端到str[i]位置的长度，比如以str[i]为中心的最长回文串是str[l,r]，那么Len[i]=r-i+1

转换后的字符串str	#	a	#	b	#	a	#	b	#	c	#
Len	1	2	1	4	1	4	1	2	1	2	1

Len[i]数组有一个性质，Len[i]-1就等于该回文串在原串s中的长度

证明：在转换后的字符串str中，所有的回文串的长度都是奇数，那么对于以str[i]为中心的最长回文串的长度为2*Len[i]-1,其中又有Len[i]个分隔符，所以在原字符串中的长度就是Len[i]-1，那么剩下的工作就是求Len数组

二、Len数组的计算

从左往右开始计算，假设0<=j<=i，那么在计算Len[i]时，Len[j]已经计算过了，设mx为之前计算过的最长回文串的右端点，id为取得这个端点值得位置（那么Len[id]=mx-id+1）

第一种情况：i<=mx.

找到i相对于id的对称位置，设为j，再次分为两种情况：

1、Len[j]<mx-i

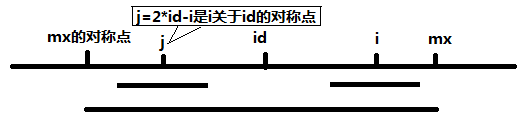
mx的对称点为2*id-mx,i和j所包含的范围是2*Len[j]-1

那么说明以j为中心的回文串一定在以id为中心的回文串内部，且i和j关于id对称，由回文串的定义可知，一个回文串反过来仍是回文串，所以以i为中心的回文串长度至少和以i为中心的回文串长度相等，即Len[i]>=Len[j].因为Len[j]<mx-i所以i+Len[j]<mx，由对称性可知Len[i]=Len[j].

2、Len[j]>=mx-i

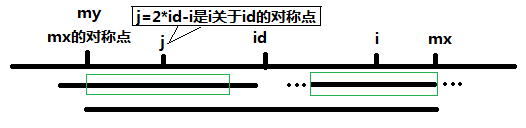
由对称性说明以i为中心的回文串可能延伸到mx之外，而大于mx的部分我们还没有进行匹配，所以要从mx+1位置开始一个一个匹配直到失配，从而更新mx和对应的id以及Len[i]

第二种情况，i>mx

如果i比mx还大，说明对于中点为i的回文串一点都没匹配，这个时候只能一个个匹配（滑稽），匹配完成后更新mx的位置和对应的id及Len[i].

代码实现：

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int maxn=1e6+;
char s[maxn*],str[maxn*];
int Len[maxn*],len;

void getstr()
{
    int k=;
    str[k++]='$';
    for(int i=;i<len;i++)
        str[k++]='#',
        str[k++]=s[i];
    str[k++]='#';
    len=k;
}
void Manacher()
{
    getstr();
    int mx=,id;
    for(int i=;i<len;i++)
    {
        if(mx>i) Len[i]=min(Len[*id-i],mx-i);
        else Len[i]=;
        while(str[i+Len[i]]==str[i-Len[i]])
            Len[i]++;
        if(Len[i]+i>mx)
            mx=Len[i]+i,id=i;
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%s",&s);
        len=strlen(s);
        Manacher();
        int ans=;
        for(int i=;i<len;i++) ans=max(ans,Len[i]);
        printf("%d\n",ans-);
    }
    return ;
}