最近公共祖先（LCT）

来一发\(LCT\)求\(LCA\)

\(LCT\)在时间上不占据优势，码量似乎还比树剖，倍增，\(Tarjan\)大一点

但是却是一道\(LCT\)的练手题

对于每一个询问，我们只需要把其中一个点（我们设为a）先\(access\)，这样a到根节点的路径就都在一棵\(Splay\)里面了

而且不难发现，有一个很妙的性质：如果两个点不在一条路径上（即\(lca!=a||lca!=b\)）那么b点\(access\)以后，b第一次到a到\(root\)的\(Splay\)的上的点即为\(LCA\)

然后我们考虑在将另一个点（我们设为b）与根的路径打通，我们还是一样一直\(Splay\)，对于最后一棵\(Splay\)

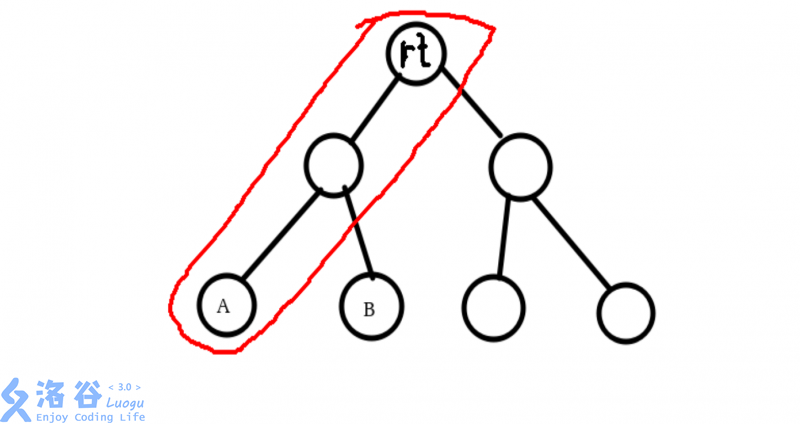
\(LCA\)即为b第一次到a和rt的那一棵\(Splay\)的位置

那么a，b本来在一个\(Splay\)上呢？

其实也是一样的，我们在分类讨论

1）若\(dep[a]>dep[b]\)那么显然不影响答案，答案就是b点

2）若\(dep[a]<dep[b]\)那么我们在\(access(a)\)时候，a，b就已经不在一颗\(Splay\)里了，所以也不影响答案

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define re register
il int read()
{
    re int x = 0, f = 1; re char c = getchar();
    while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
#define get_fa(x) (ch[1][fa[x]] == x)
#define isroot(x) (ch[1][fa[x]] == x || ch[0][fa[x]] == x)
#define updown(x) swap(ch[1][x], ch[0][x]), tag[x] ^= 1
#define rep(i, s, t) for(re int i = s; i <= t; ++ i)
#define maxn 500005
int n, m, s, ch[2][maxn], fa[maxn], st[maxn], top, tag[maxn];
il void pushdown(int x)
{
    if(tag[x])
    {
        if(ch[0][x]) updown(ch[0][x]);
        if(ch[1][x]) updown(ch[1][x]);
        tag[x] = 0;
    }
}
il void rotate(int x)
{
    int y = fa[x], z = fa[y], w = get_fa(x), k = get_fa(y);
    if(isroot(y)) ch[k][z] = x;
    if(ch[w ^ 1][x]) fa[ch[w ^ 1][x]] = y;
    fa[x] = z, fa[y] = x;
    ch[w][y] = ch[w ^ 1][x], ch[w ^ 1][x] = y;
}
il void Splay(int x)
{
    int y = x;
    st[++ top] = x;
    while(isroot(y)) st[++ top] = y = fa[y];
    while(top) pushdown(st[top --]);
    while(isroot(x))
    {
        int y = fa[x];
        if(isroot(y)) rotate(get_fa(x) == get_fa(y) ? y : x);
        rotate(x);
    }
}
il void access(int x)
{
    for(re int y = 0; x; x = fa[y = x]) Splay(x), ch[1][x] = y;
}
il void makeroot(int x) {access(x), Splay(x), updown(x);}
il void link(int a, int b) {makeroot(a), fa[a] = b;}
il int query(int a, int b)
{
    access(a);
    int ans = 0;
    for(; b; b = fa[ans = b]) Splay(b), ch[1][b] = ans;
    return ans;
}
int main()
{
    n = read(), m = read(), s = read();
    rep(i, 1, n - 1){int u = read(), v = read(); link(u, v);}
    makeroot(s);
    while(m --)
    {
        int a = read(), b = read();
        printf("%d\n", query(a, b));
    }
    return 0;
}