uva 1411 Ants

题意：

一个平面上有n个黑色的点，n个白色的点，要求黑色的点与白色点之间一一配对，且线段之间不相交。

思路：

线段不相交并不好处理，想了很久想不出，所以看了蓝书的讲解。

一个很明显的结论是，不相交的线段一定比相交的线段短，如图：一个较为直观的例子。

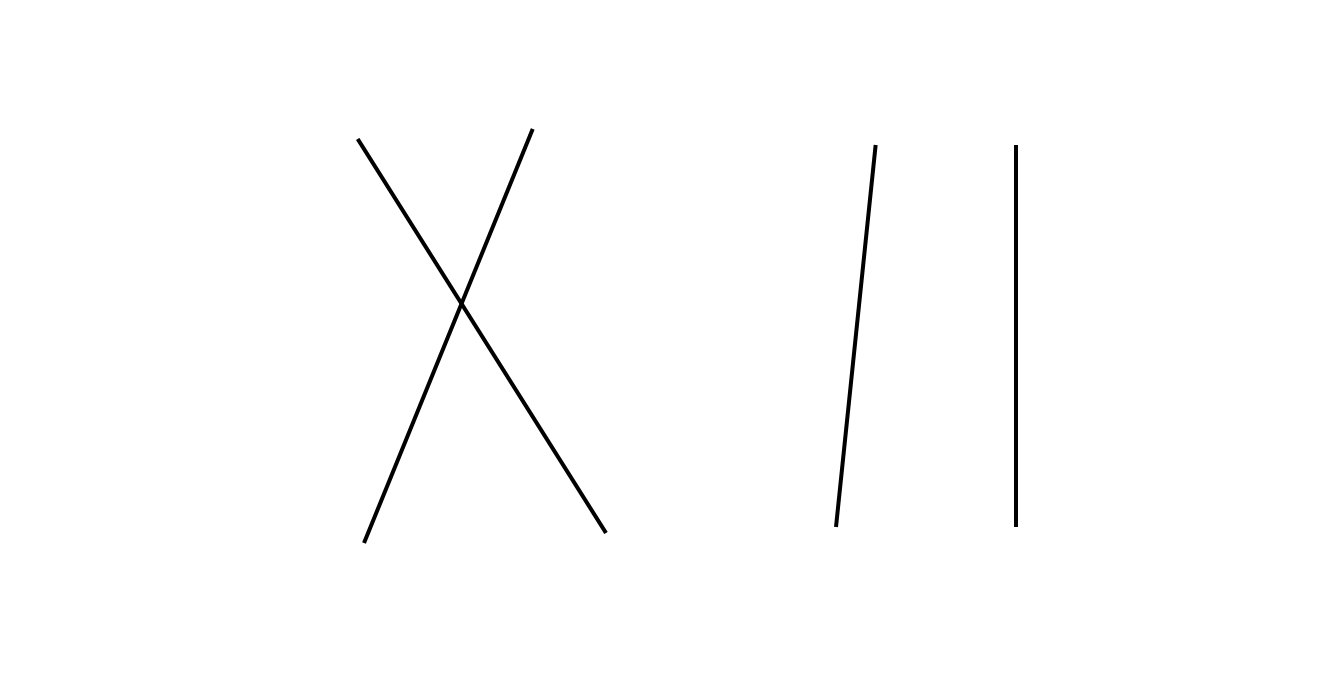
由于点之间一一对应，所以肯定用二分图匹配，然后要使得所有线段之和最短，那么就是求一个带权最小匹配，上KM算法解决。

把所有的边权取负值，求最大匹配即可。

代码：

 #include <stdio.h>
 #include <math.h>
 #include <string.h>
 #include <algorithm>
 #include <vector>
 using namespace std;

 const int N = ;

 double mp[N][N];

 struct node
 {
     double x,y;
     node(double a,double b)
     {
         x = a;
         y = b;
     }
 };

 vector<node> nx,ny;

 bool vis_x[N],vis_y[N];
 int match[N];
 double lx[N],ly[N];
 double slack[N];
 int ma[N];

 double cal(int i,int j)
 {
     double dx = pow(nx[i].x - ny[j].x,);
     double dy = pow(nx[i].y - ny[j].y,);

     return sqrt(dx + dy);
 }

 bool dfs(int u,int n)
 {
     vis_x[u] = ;

     for (int i = ;i < n;i++)
     {
         if (vis_y[i]) continue;

         double gap = lx[u] + ly[i] - mp[u][i];

         //getchar();

         //printf("%.6f %.6f %.6f %.6f\n",lx[u],ly[i],mp[u][i],gap);

         if (fabs(gap) < 1e-)
         {
             vis_y[i] = ;

             if (match[i] == - || dfs(match[i],n))
             {
                 match[i] = u;
                 return true;
             }
         }
         else
         {
             slack[i] = min(slack[i],gap);
         }
     }

     return false;
 }

 void km(int n)
 {
     memset(ly,,sizeof(ly));
     memset(match,-,sizeof(match));

     for (int i = ;i < n;i++)
     {
         lx[i] = mp[i][];

         for (int j = ;j < n;j++)
         {
             lx[i] = max(lx[i],mp[i][j]);
         }
     }

     for (int i = ;i < n;i++)
     {
         for (int j = ;j < n;j++) slack[j] = 1e15;
         //printf("gg");
         while ()
         {
             //printf("233");
             memset(vis_x,,sizeof(vis_x));
             memset(vis_y,,sizeof(vis_y));

             if (dfs(i,n)) break;

             double d = 1e15;

             for (int j = ;j < n;j++)
             {
                 if (!vis_y[j]) d = min(slack[j],d);
             }

             for (int j = ;j < n;j++)
             {
                 if (vis_x[j]) lx[j] -= d;

                 if (vis_y[j]) ly[j] += d;
             }

             //getchar();

             //printf("%.6f **\n",d);
         }
     }
 }

 int main()
 {
     int n;
     int kase = ;

     while (scanf("%d",&n) != EOF)
     {
         if (kase++) printf("\n");

         nx.clear();
         ny.clear();

         for (int i = ;i < n;i++)
         {
             double x,y;
             scanf("%lf%lf",&x,&y);

             nx.push_back(node(x,y));
         }

         for (int i = ;i < n;i++)
         {
             double x,y;
             scanf("%lf%lf",&x,&y);

             ny.push_back(node(x,y));
         }

         for (int i = ;i < n;i++)
         {
             for (int j = ;j < n;j++)
             {
                 mp[i][j] = -cal(i,j);
             }
         }

         km(n);

         for (int i = ;i < n;i++)
         {
             int a = i + ,b = match[i] + ;
             ma[b] = a;
         }

         for (int i = ;i < n;i++)
         {
             printf("%d\n",ma[i+]);
         }
     }

     return ;
 }