直线的参数方程ABC

直线的参数方程的来源

如图所示，

直线\(l\)的倾斜角为\(\theta\)，经过定点\(P_0(x_0,y_0)\)，在直线上有一动点\(P(x，y)\),如果我们取直线的单位方向向量\(\vec e=(cos\theta,sin\theta)\),由平面向量共线定理可知，存在唯一确定的常数\(t\)，使得向量\[\overrightarrow{P_0 P}=t\cdot \vec e\]即 \[(x-x_0，y-y_0)=t(cos\theta,sin\theta)，\]即 \[ x-x_0=t\cdot cos\theta ，y-y_0=t\cdot sin\theta, \]这样直线上的任意一个动点\(P\)的坐标可以表示为

\begin{cases} x=x_0+cos\theta\cdot t \\ y=y_0+sin\theta\cdot t (t为参数) \end{cases}

我们称上式为倾斜角为\(\theta\)，经过定点\(P_0(x_0,y_0)\)的直线\(l\)的参数方程。
等等，让我们慢慢的捋一捋，问题来了：

【问题1】\(t\)的几何意义是什么？如果我们当时取得方向向量不是单位向量，又会如何？

答：当我们取的是单位方向向量，则由向量共线定理知道，向量\(|\overrightarrow{P_0 P}|=|\vec e||t|=|t|\)，故\(t\)的几何意义是有向线段\(P_0P\)的数量；如果当时取的不是单位向量，则\(t\)不是有向线段\(P_0P\)的数量。

【问题2】\(t\)一定为正值吗？

答：\(t\)为0，为正，为负都可以，如上图，\(t>0\)；\(P\)和\(P_0\)重合时，\(t=0\)；如果我们当时取的单位方向向量和\(\vec e\)相反，则\(t<0\)。

【问题3】给定倾斜角和定点坐标，你能仿上写出直线的参数方程吗？

答：如已知给定直线的倾斜角为\(\beta=\cfrac{\pi}{3}\)，过定点\(A(2，1)\)，则我们可以写出参数方程为

\begin{cases} x=2+cos\cfrac{\pi}{3}\cdot m \\\ y=1+sin\cfrac{\pi}{3}\cdot m (m为参数) \end{cases}

【问题4】给定直线的参数方程，你能找出倾斜角和定点坐标吗？

答：如给定

\begin{cases} x=-1+\cfrac{\sqrt{2}}{2}\cdot n \\ y=\cfrac{\sqrt{2}}{2}\cdot n (n为参数) \end{cases}

则我们可以知道倾斜角为\(\cfrac{\pi}{4}\)，过定点\((-1，0)\)，

如果给定

\begin{cases} x=-1+\cfrac{\sqrt{2}}{2}\cdot n \\ y=2-\cfrac{\sqrt{2}}{2}\cdot n (n为参数) \end{cases}

你都能用什么思路求得定点坐标和倾斜角？

定点的坐标容易求解，是\((-1，2)\)，但是倾斜角的求解需要注意：思路1：必须把参数方程变换为

\begin{cases} x=-1-\cfrac{\sqrt{2}}{2}\cdot n \\ y=2+\cfrac{\sqrt{2}}{2}\cdot n (n为参数) \end{cases}

所以倾斜角是\(\cfrac{3\pi}{4}\)，为什么要调整？由原来的参数方程的直接得到的倾斜角是\(\cfrac{7\pi}{4}\notin [0，2\pi)\)，需要往回旋转\(\pi\)。

【问题5】是不是随便给一个直线的参数方程，\(t\)的几何意义都是这样的？

答：不是的，如给定

\begin{cases} x=-1+ n \\ y=1- n (n为参数) \end{cases}

\(n\)的几何意义不是有向线段\(P_0P\)的数量，这种形式只是直线的参数方程的一般形式，需要转换为标准形式。

【问题6】如何把一个直线的参数方程的一般式转化为标准式？

答：我们注意到

\begin{cases} x=x_0+cos\theta\cdot t \\ y=y_0+sin\theta\cdot t (t为参数) \end{cases}

方程组中的参数\(t\)的两个系数的平方和是1，即\(cos^2\theta+sin^2\theta=1\)，这就保证了选取的向量是单位向量，如上给定

\begin{cases} x=-1+ n \\ y=1- n (n为参数) \end{cases}

说明选取的向量坐标是\(（1，-1）\)，那么转换为单位向量是\((\cfrac{1}{\sqrt{2}},-\cfrac{1}{\sqrt{2}})\)，即\((\cfrac{\sqrt{2}}{2},-\cfrac{\sqrt{2}}{2})\)，这样参数方程的一般式就可以改写为标准式

\begin{cases} x=-1+\cfrac{\sqrt{2}}{2}\cdot m \\ y=1-\cfrac{\sqrt{2}}{2}\cdot m (m为参数) \end{cases}

，这样我们就能放心的利用直线参数方程的\(m\)的几何意义解题了。

具体的变换如下：

\begin{cases} x=-1+ n=-1+\cfrac{\sqrt{2}}{2}(\sqrt{2}n)=-1+\cfrac{\sqrt{2}}{2}m \\\ y=1- n=1-\cfrac{\sqrt{2}}{2}(\sqrt{2}n)=1-\cfrac{\sqrt{2}}{2}m (m为参数,m=\sqrt{2}n) \end{cases}

即

\begin{cases} x=-1+\cfrac{\sqrt{2}}{2}m \\ y=1-\cfrac{\sqrt{2}}{2}m (m为参数) \end{cases}

【问题7】我们为什么要学习参数方程，参数方程比之其他方程有什么好处？

答：参数方程的参数一般都是有其对应的几何意义，所以利用其几何意义可以解决一部分问题，这是优越性之一；
其二有了参数的介入，使得方程中的未知数之间的的关系变得间接化，这在直线的参数方程中体现的不是很明显，在圆的参数方程中就体现的非常明显，如\(x^2+y^2=1\)，引入参数\(\theta\)后，圆上的动点的坐标就是\((cos\theta，sin\theta)\),比如在求解圆上的点到直线的最短距离就非常的方便；再比如，解三角形中，如果已知\(a:b:b=3:2:4\)，如果我们引入参数\(k（k>0）\)，则可以方便的单独表示\(a=3k，b=2k，c=4k\)。

【问题8】直线上的任意一个动点\(P\)，都有唯一的参数\(t\)与之对应，对吗，为什么？

【举例】利用直线参数方程的参数的几何意义解题

引例如，在极坐标系中，已知圆\(C\)的圆心\(C(\sqrt{2}，\cfrac{\pi}{4})\)，半径\(r=\sqrt{3}\)，

（1）求圆\(C\)的极坐标方程。

（2）若\(\alpha \in[0,\cfrac{\pi}{4}]\)，直线\(l\)的参数方程为

\begin{cases} x=2+cos\alpha\cdot t \\ y=2+sin\alpha\cdot t (t为参数) \end{cases}

直线\(l\)交圆\(C\)于\(A、B\)两点，求弦长\(|AB|\)的取值范围。

解：（1）圆\(C\)的圆心\(C(\sqrt{2}，\cfrac{\pi}{4})\)，得\(C\)的直角坐标为\((1,1)\)，所以圆\(C\)的直角坐标方程为\((x-1)^2+(y-1)^2=3\)，由\(x=\rho cos\theta,y=\rho sin\theta\)得到，圆\(C\)的极坐标方程为\(\rho^2-2\rho cos\theta-2\rho sin\theta-1=0\)。

（2）将

\begin{cases} x=2+cos\alpha\cdot t \\ y=2+sin\alpha\cdot t (t为参数) \end{cases}

代入圆\(C\)的直角坐标方程为\((x-1)^2+(y-1)^2=3\)，得到\(t^2+2(cos\alpha+sin\alpha)t-1=0\)，则有\(\Delta= 4(cos\alpha+sin\alpha)^2+4>0\)，

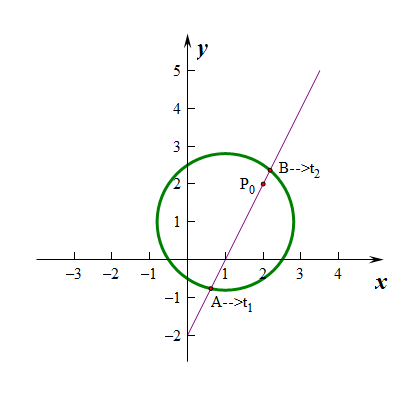
设\(A、B\)两点对应的参数分别为\(t_1，t_2\)，则由韦达定理可知，\(t_1+t_2=2(cos\alpha+sin\alpha)，t_1\cdot t_2= -1\)

所以弦长\(|AB|=|t_1-t_2|=\sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{8+4sin2\alpha}\)，由于\(\alpha \in[0,\cfrac{\pi}{4}]\)，所以\(sin2\alpha\in[0，1]\)，\(8+4sin2\alpha\in[8，12]\)，所以弦长\(|AB|\in[2\sqrt{2}，2\sqrt{3}]\)。

【几个重要的结论】

1、

2、

3、

4、

5、