【LeetCode】892. Surface Area of 3D Shapes 解题报告（Python）

作者： 负雪明烛
id： fuxuemingzhu
个人博客： http://fuxuemingzhu.cn/

---

目录

• • 题目描述
  • 题目大意
  • 解题方法
  • 日期

题目地址：https://leetcode.com/problems/surface-area-of-3d-shapes/description/

题目描述

On a N * N grid, we place some 1 * 1 * 1 cubes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).

Return the total surface area of the resulting shapes.

Example 1:

Input: [[2]]
Output: 10

Example 2:

Input: [[1,2],[3,4]]
Output: 34

Example 3:

Input: [[1,0],[0,2]]
Output: 16

Example 4:

Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 32

Example 5:

Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 46

Note:

1. 1 <= N <= 50
2. 0 <= grid[i][j] <= 50

题目大意

所给出的数组是每个坐标下的z值，求整个空间图形的表面积。

解题方法

这个题乍一看和883. Projection Area of 3D Shapes非常相像。甚至我以为就是883题的答案乘以2就行。。但是我看到了第5个例子之后，眉头一皱发现事情并不简单。

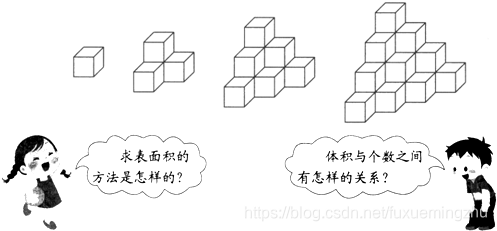
实际上，要求整个图形的表面积，那么可以分解为求出每个立方体的表面积，然后减去重叠部分的面积就可以。按照这个思路，就变得简单了。

1. 当只有1个立方体的时候，表面积是6；
2. 如果有多个立方体摞在一起成为柱子的时候，表面积是grid[i][j] * 4 + 2；
3. 如果有多个柱子的时候，需要减去重叠面积。重叠的高度是两个柱子之间，高度最小的那个的高度。因为重叠使得两个柱子都变矮了，所以要把这个高度*2.

举个例子：

对于第一个例子，输入只有一个柱子，柱子的高度是2，那么表面积是2 * 4 + 2 = 10。

再举个栗子

1,2
3,4

计算的时候是这样的：

• 首先看柱子1，表面积是6；
• 当添加柱子2，其表面积是2 * 4 + 2 = 10，但是由于和左边的1有重叠，重叠面积是2，所以添加柱子2之后，总的表面积是6 + 10 - 2 = 14;
• 当添加柱子3，柱子3的表面积是3 * 4 + 2 = 14，由于和柱子1有重叠，重叠面积是2，所以添加柱子3之后，总面积是14 + 14 - 2 = 26；
• 当添加柱子4，柱子4的表面积是4 * 4 + 2 = 18，由于和柱子2和3有重叠，重叠面积是(2 + 3) * 2 = 10，所以添加柱子4之后，总面积是26 + 18 - 10 = 34。

Python代码如下：

class Solution(object):
    def surfaceArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        area = 0
        n = len(grid)
        for i in range(n):
            for j in range(n):
                if grid[i][j]: area += grid[i][j] * 4 + 2
                if i: area -= min(grid[i][j], grid[i-1][j]) * 2
                if j: area -= min(grid[i][j], grid[i][j-1]) * 2
        return area

---

二刷的写法如下。

class Solution(object):
    def surfaceArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        count = 0
        inner = 0
        M, N = len(grid), len(grid[0])
        for i in range(M):
            for j in range(N):
                count += grid[i][j]
                if i < M - 1 and grid[i + 1][j] != 0:
                    inner += min(grid[i][j], grid[i + 1][j])
                if j < N - 1 and grid[i][j + 1] != 0:
                    inner += min(grid[i][j], grid[i][j + 1])
                if grid[i][j] >= 2:
                    inner += grid[i][j] - 1
        print(count, inner)
        return count * 6 - inner * 2

C++代码如下：

class Solution {
public:
    int surfaceArea(vector<vector<int>>& grid) {
        int res = 0;
        int N = grid.size();
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                res += grid[i][j] * 6 - max(0, grid[i][j] - 1) * 2;
                if (i != 0) {
                    res -= min(grid[i - 1][j], grid[i][j]) * 2;
                }
                if (j != 0) {
                    res -= min(grid[i][j - 1], grid[i][j]) * 2;
                }
            }
        }
        return res;
    }
};

日期

2018 年 8 月 26 日 ———— 珍爱生命，远离DD！
2018 年 11 月 ９ 日 —— 睡眠可以
2020 年 3 月 25 日 —— 想发财