扩展kmp 学习笔记

学习了一下这个较为冷门的知识，由于从日报开始看起，还是比较绕的……

首先定义 \(Z\) 函数表示后缀 \(i\) 与整个串的 \(lcp\) 长度

一个比较好的理解于实现方式是类似于 \(manacher\) 维护出 \([l,r]\) 表示能够匹配的最右端是 \(l\) 位置匹配上的到达 \(r\) 的区间

假设目前求到 \(i\)：

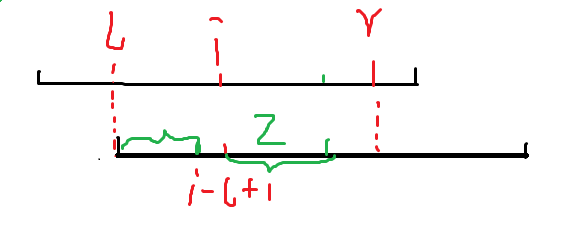
那么可以发现可以直接由 \(nxt[i-l+1]\) 继承过来，需要和 \(r-i+1\) 取 \(min\)

另一个问题是假如 \(r<i\) 或 \(nxt[i-l+1]\ge r-i+1\)，后面的部分需要进行暴力匹配

并且及时更新 \(r\) 的取值

以下是模板实现：

代码实现

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e7+5;
int n,m,nxt[maxn],ex[maxn];
char a[maxn],b[maxn];
long long ans;
void getnxt(){
	nxt[1]=m;
	for(int i=2,l=0,r=0;i<=m;i++){
		if(i<=r)nxt[i]=min(nxt[i-l+1],r-i+1);
		while(i+nxt[i]<=m&&b[nxt[i]+i]==b[nxt[i]+1])nxt[i]++;
		if(i+nxt[i]-1>r)r=i+nxt[i]-1,l=i;
	}
	return ;
}
void exkmp(){
	for(int i=1,l=0,r=0;i<=n;i++){
		if(i<=r)ex[i]=min(nxt[i-l+1],r-i+1);
		while(i+ex[i]<=n&&a[ex[i]+i]==b[ex[i]+1])ex[i]++;
		if(i+ex[i]-1>r)l=i,r=i+ex[i]-1;
	}
	return ;
}
int main(){
	scanf("%s%s",a+1,b+1);
	n=strlen(a+1),m=strlen(b+1);
	getnxt();exkmp();
	for(int i=1;i<=m;i++)ans^=1ll*i*(nxt[i]+1);cout<<ans<<endl;//printf("%d ",nxt[i]);puts("");
	ans=0;for(int i=1;i<=n;i++)ans^=1ll*i*(ex[i]+1);cout<<ans;
	return 0;
}

---

CF432D Prefixes and Suffixes

相当于比较每个后缀的 \(nxt\) 值是否等于后缀长度

由于需要求出现的次数，不妨还是把后缀们平移到前缀的位置

那么发现一个前缀出现的次数是后面前缀出现次数的前缀和

代码实现

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
char a[maxn];
int nxt[maxn],ans,cnt[maxn];
bool vis[maxn];
int main(){
	scanf("%s",a+1);
	int n=strlen(a+1);
	nxt[1]=n;
	for(int i=2,l=0,r=0;i<=n;i++){
		if(i<=r)nxt[i]=min(nxt[i-l+1],r-i+1);
		while(nxt[i]+i<=n&&a[nxt[i]+i]==a[nxt[i]+1])nxt[i]++;
		if(nxt[i]+i-1>r)r=nxt[i]+i-1,l=i;
	}
	for(int i=1;i<=n;i++){
		if(i+nxt[i]-1==n)ans++,vis[nxt[i]]=true;
		cnt[nxt[i]]++;
	}
	for(int i=n;i>=1;i--)cnt[i]+=cnt[i+1];
	cout<<ans<<endl;
	for(int i=1;i<=n;i++)if(vis[i])printf("%d %d\n",i,cnt[i]);
	return 0;
}