zabbix保姆级安装教程

安装步骤

1.进入官网选择下载的版本和服务器类型

官网地址：https://www.zabbix.com/cn/download?zabbix=5.0&os_distribution=centos&os_version=7&db=mysql&ws=apache

以5.0版本为例

2.安装zabbix服务器

输入：

rpm -Uvh https://repo.zabbix.com/zabbix/5.0/rhel/7/x86_64/zabbix-release-5.0-1.el7.noarch.rpm

3.安装 Zabbix 服务器和代理

输入：

yum install zabbix-server-mysql zabbix-agent

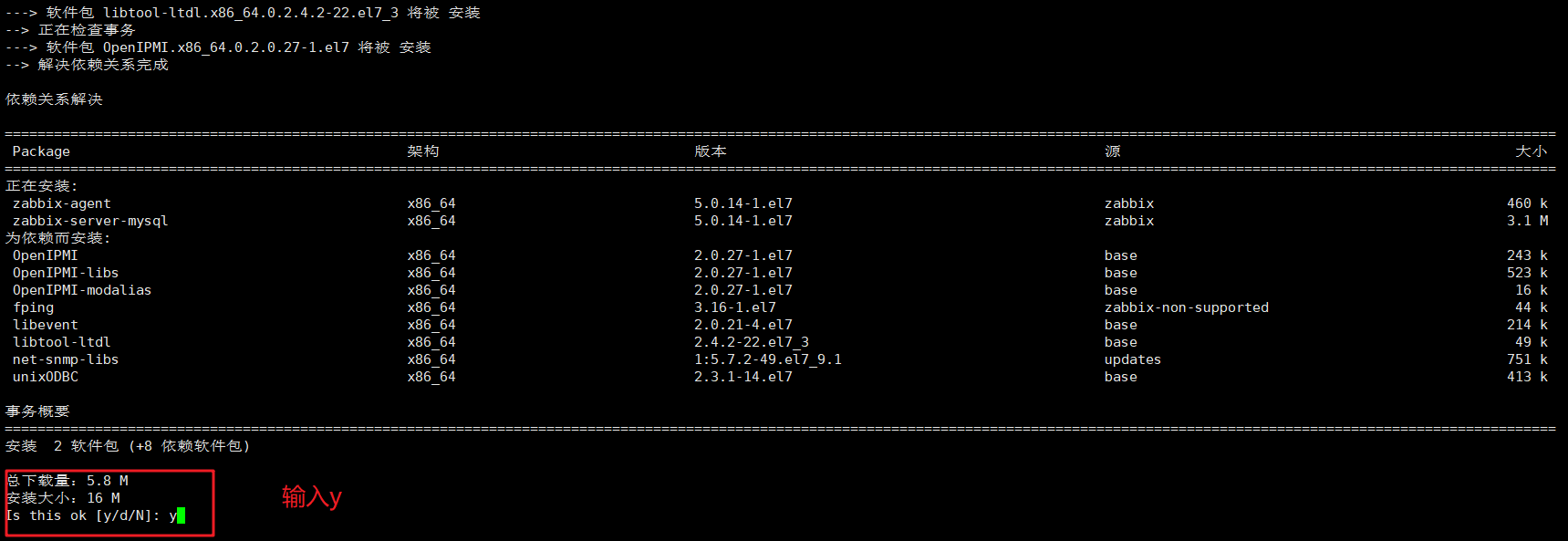
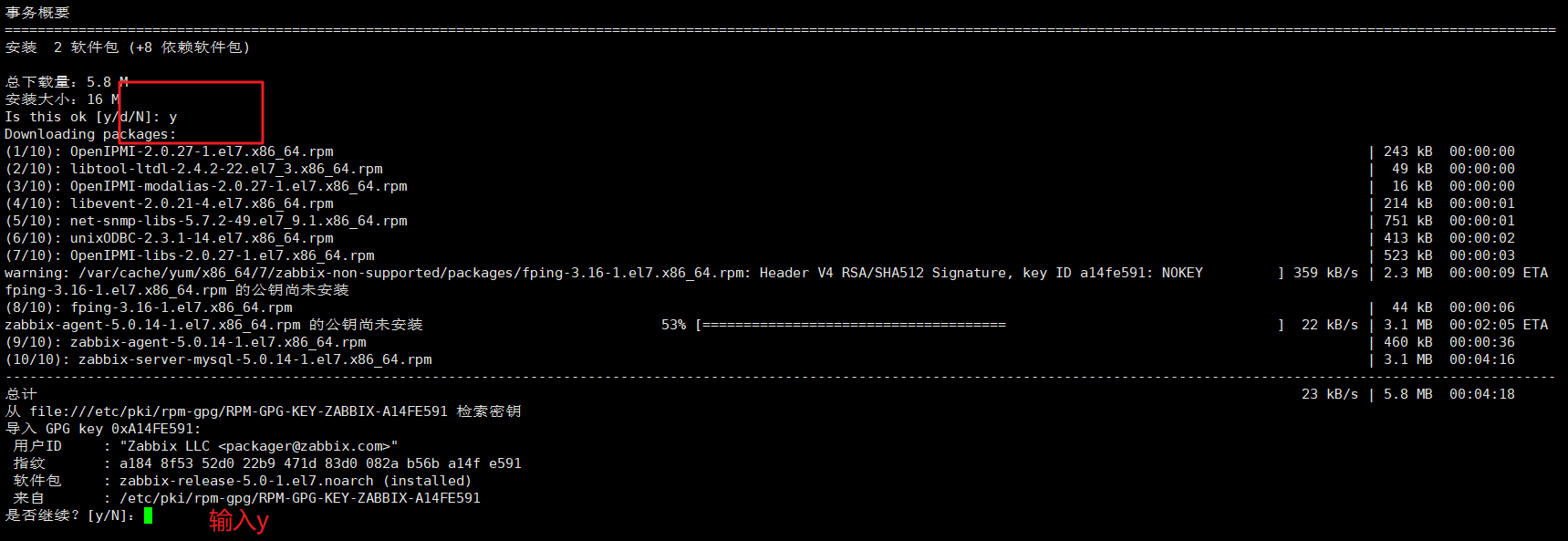
4.安装zabbix前端

输入：

yum install centos-release-scl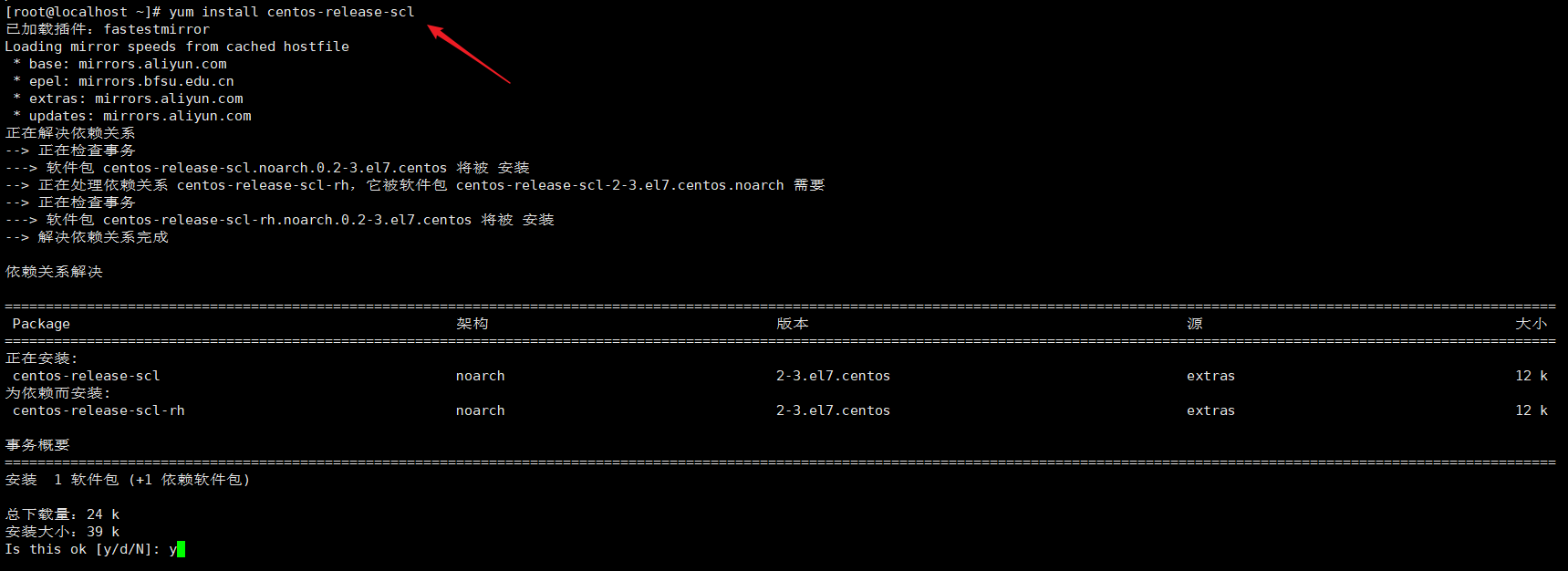

5.编辑配置文件

输入：

vi /etc/yum.repos.d/zabbix.repo and enable zabbix-frontend repository

将 enabled=0 改成 enabled=1

[zabbix-frontend]
...
enabled=1
...

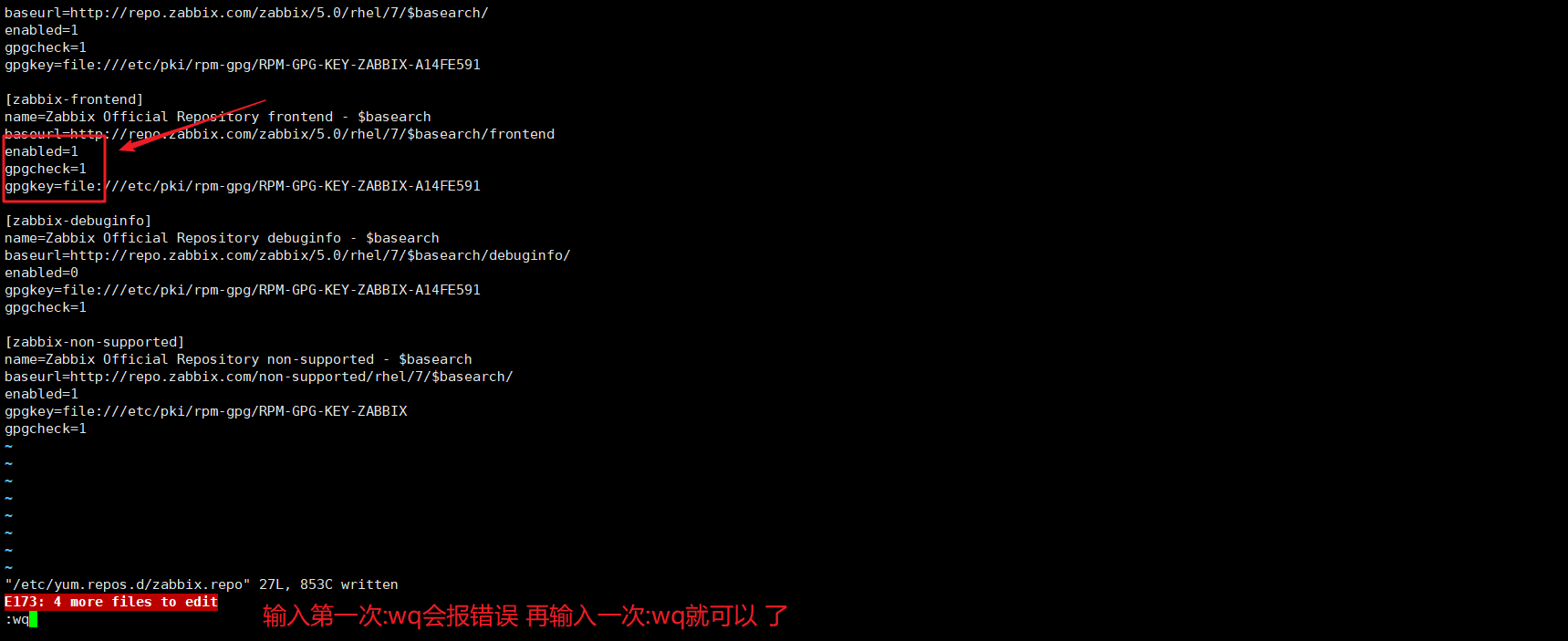
6.安装zabbix前端包

输入：

yum install zabbix-web-mysql-scl zabbix-apache-conf-scl

遇到询问就输入y

7.创建数据库

前提：服务器中已经存在可以运行的数据库

7.1 进入数据库

# mysql -uroot -p
(mysql密码)

## 新建一个表名为zabbix（自定义）的数据表
mysql>create database zabbix character set utf8 collate utf8_bin;
## 新建一个用户名为zabbix@localhost（自定义）并设置密码（密码应该包含大小写数字特殊字符）不然密码不能通过
mysql>create user zabbix@localhost identified by 'password';
## 给zabbix@localhost用户授予zabbix表的权限
mysql>grant all privileges on zabbix.* to zabbix@localhost;
## 退出
mysql>quit

密码示例： Zabbix_123  数据库新建用户时

7.2 导入初始架构和数据，系统将提示您输入新创建的密码。

zcat /usr/share/doc/zabbix-server-mysql*/create.sql.gz | mysql -uzabbix -p zabbix

ENTER Password (输入自己设置的密码)

这里耐心等一下 ：导入时间比较长

8.为zabbix Server 配置数据库

vi /etc/zabbix/zabbix_server.conf

DBPassword=password(之前设置的密码)

如果配置文件内容太多  可以通过  /搜索内容  进行快速定位
注意：插入状态不能进行搜索

9.启动Zabbix server和agent进程

systemctl restart zabbix-server zabbix-agent httpd rh-php72-php-fpm

遇到的问题：

如果这里启动失败的话 多半是因为端口被占用了 可以先停掉占用端口的进程，再执行启动命令

10.设置开机自启动

systemctl enable zabbix-server zabbix-agent httpd rh-php72-php-fpm