2021.9.7考试总结[NOIP模拟49]

T1 Reverse

---

$BFS$暴力$O(n^2)$

过程中重复枚举了很多点，考虑用链表记录当前点后面可到达的第一个未更新点。

搜索时枚举翻转子串的左端点，之后便可以算出翻转后$1$的位置。

$code:$

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3
 4 namespace IO{
 5     inline int read(){
 6         char ch=getchar(); int x=0,f=1;
 7         while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
 8         while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
 9         return x*f;
10     }
11     inline void write(int x,char sp){
12         char ch[20]; int len=0;
13         if(x<0){ putchar('-'); x=~x+1; }
14         do{ ch[len++]=x%10+(1<<4)+(1<<5); x/=10; }while(x);
15         for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
16     }
17     inline int max(int x,int y){ return x<y?y:x; }
18     inline int min(int x,int y){ return x<y?x:y; }
19     inline void swap(int &x,int &y){ x^=y^=x^=y; }
20     inline void chmax(int &x,int y){ x=x<y?y:x; }
21     inline void chmin(int &x,int y){ x=x<y?x:y; }
22 } using namespace IO;
23
24 const int NN=1e5+5;
25 int n,m,s,k,dis[NN],nex[NN];
26 bool ban[NN];
27 vector<int>move;
28
29 void bfs(){
30     memset(dis,-1,sizeof(dis));
31     queue<int>q;
32     for(int i=1;i<=n;i++) nex[i]=i+2;
33     dis[s]=0; q.push(s);
34     while(!q.empty()){
35         int x=q.front(),l=max(1,x-k+1),r=min(x,n-k+1),tmp;
36         for(int i=2*l+k-x-1;i<=2*r+k-x-1;i=tmp){
37             tmp=nex[i]; nex[i]=nex[2*r+k-x-1];
38             if(i>n||ban[i]||dis[i]>=0) continue;
39             dis[i]=dis[x]+1; q.push(i);
40         }
41         q.pop();
42     }
43 }
44
45 signed main(){
46     n=read(); k=read(); m=read(); s=read();
47     for(int i=1;i<=m;i++) ban[read()]=1;
48     bfs();
49     for(int i=1;i<=n;i++) write(dis[i],' ');
50     return 0;
51 }

T1

T2 Silhouette

---

首先每一行与每一列都有交点，所以排序不影响方案数。于是先将$a,b$排序。如果$a_{max} \neq b_{max}$则无解。

考虑从大到小枚举$a,b$的值$s$，考虑$min(a_i,b_j)=s$的情况，那么每次考虑的位置会构成一个$L$形或矩形。而矩形又可以看作特殊的$L$。

对于$s_{max}$，考虑范围是右上角的矩形。考虑容斥，设$f_i$为矩形中至少$i$行不合法的方案数，令矩形$a$行$b$列，则有

$f[i]=C_a^i\times (S^i\times ((S+1)^{a-i}-S^{a-i}))^b$。

答案即为$\sum_{i=0}^a (-1)^i \times f_i$。

再考虑普遍情况。考虑如下图形

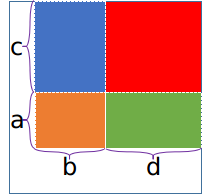
其中红色部分已满足行列要求。因此蓝色部分不能不满足行要求，绿色部分不能不满足列要求。

可以将蓝橙绿分为蓝橙和绿两部分分别计算。蓝橙部分类似特殊情况，但只有橙部分可能不合法。此后绿部分行列要求已被橙红两块满足，随便选即可。

令$f_i$为$a$中有至少$i$行不合法，有

$f[i]=C_a^i\times (S^i\times ((S+1)^{a+c-i}-S^{a+c-i}))^b\times (S^i\times (S+1)^{a-i})^d$

一样容斥，最后累乘即可。

$code:$

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4
 5 namespace IO{
 6     inline int read(){
 7         char ch=getchar(); int x=0,f=1;
 8         while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
 9         while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
10         return x*f;
11     }
12     inline void write(int x,char sp){
13         char ch[20]; int len=0;
14         if(x<0){ putchar('-'); x=~x+1; }
15         do{ ch[len++]=x%10+(1<<4)+(1<<5); x/=10; }while(x);
16         for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
17     }
18     inline int max(int x,int y){ return x<y?y:x; }
19     inline int min(int x,int y){ return x<y?x:y; }
20     inline void swap(int &x,int &y){ x^=y^=x^=y; }
21     inline void chmax(int &x,int y){ x=x<y?y:x; }
22     inline void chmin(int &x,int y){ x=x<y?x:y; }
23 } using namespace IO;
24
25 const int NN=1e5+5,p=1e9+7;
26 int n,ans,ext,tma,tmb,pra,prb,a[NN],b[NN],s[NN<<1];
27
28 namespace math{
29     int fac[NN],inv[NN];
30     inline int C(int x,int y){
31         if(x<y) return 0;
32         return fac[x]*inv[y]%p*inv[x-y]%p;
33     }
34     inline int qpow(int x,int y){
35         int res=1;
36         while(y){
37             if(y&1) res=res*x%p;
38             x=x*x%p;
39             y>>=1;
40         }
41         return res;
42     }
43     void init(){
44         fac[0]=inv[0]=1;
45         for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%p;
46         inv[n]=qpow(fac[n],p-2);
47         for(int i=n-1;i;i--) inv[i]=inv[i+1]*(i+1)%p;
48     }
49 } using namespace math;
50
51 inline int calc(int mia,int mib,int upa,int upb,int num){
52     int res=0;
53     for(int i=0;i<=mia;i++){
54         int now=C(mia,i)*qpow(qpow(num,i)*(qpow(num+1,mia+upa-i)-qpow(num,mia+upa-i)+p)%p,mib)%p;
55         now=now*qpow(qpow(num,i)*qpow(num+1,mia-i)%p,upb)%p;
56         if(i&1) now=p-now;
57         (res+=now)%=p;
58     }
59     return res;
60 }
61
62 signed main(){
63     n=read(); init(); ans=1;
64     for(int i=1;i<=n;i++) s[i]  =a[i]=read();
65     for(int i=1;i<=n;i++) s[i+n]=b[i]=read();
66     sort(a+1,a+n+1); sort(b+1,b+n+1); sort(s+1,s+2*n+1);
67     ext=unique(s+1,s+2*n+1)-s-1;
68     if(a[n]!=b[n]){ puts("0"); return 0; }
69     pra=prb=n+1; tma=tmb=n;
70     for(int i=ext;i;i--){
71         while(a[tma-1]==s[i]&&tma-1) --tma;
72         while(b[tmb-1]==s[i]&&tmb-1) --tmb;
73         (ans*=calc(pra-tma,prb-tmb,n-pra+1,n-prb+1,s[i]))%=p;
74         pra=tma; prb=tmb;
75     }
76     write(ans,'\n');
77     return 0;
78 }

T2

T3 Seat

---

skyh倾情压行注释（？

发现每次选座位区间长度的可重集是固定的，可以按照最大距离分层，然后进行$DP$。分奇偶讨论，

多理解几节课就差不多了..

不放代码了（几乎一样还放个锤子