决策树 机器学习,西瓜书p80 表4.2 使用信息增益生成决策树及后剪枝
使用信息增益构造决策树,完成后剪枝
1 构造决策树
1 根结点的选择
色泽 信息增益
根据色泽划分为 青绿,乌黑,浅白 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^2) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D^3)&= -(\frac{2}{2} log_2 \frac{2}{2}+\frac{0}{2} log_2 \frac{0}{2})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,色泽)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{4}{10}\times 1+\frac{4}{10} \times 0.811+\frac{2}{10}\times0) \\
&= 0.2756\end{aligned}
\]
根蒂 信息增益
根据根蒂划分为 蜷缩 稍蜷 硬挺 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{5} log_2 \frac{2}{5}+\frac{3}{5} log_2 \frac{3}{5})=0.971 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{5}{10}\times 0.971+\frac{4}{10} \times 1+\frac{1}{10}\times0) \\
&= 0.1145\end{aligned}
\]
敲声 信息增益
根据色泽划分为 浊响,沉闷,清脆 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{6} log_2 \frac{2}{6}+\frac{4}{6} log_2 \frac{4}{6})=0.918 \\
Ent(D^2) &= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{1}{3} log_2 \frac{1}{3})=0.918 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{6}{10}\times 0.918+\frac{3}{10} \times 0.918+\frac{1}{10}\times0) \\
&=0.2346\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 模糊 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{6} log_2 \frac{2}{6}+\frac{4}{6} log_2 \frac{4}{6})=0.918 \\
Ent(D^2) &= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{1}{3} log_2 \frac{1}{3})=0.918 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{6}{10}\times 0.918+\frac{3}{10} \times 0.918+\frac{1}{10}\times0) \\
&= 0.2346\end{aligned}
\]
脐部 信息增益
根据色泽划分为 凹陷,稍凹,平坦 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^3)&= -(\frac{2}{2} log_2 \frac{2}{2}+\frac{0}{2} log_2 \frac{0}{2})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,脐部)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{4}{10}\times 0.811+\frac{4}{10} \times 1+\frac{2}{10}\times0) \\
&= 0.2756\end{aligned}
\]
触感 信息增益
根据色泽划分为 硬滑,软粘 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{3}{6} log_2 \frac{3}{6}+\frac{3}{6} log_2 \frac{3}{6})=1 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{6}{10}\times 1 +\frac{4}{10} \times 1 \\
&= 0\end{aligned}
\]
选择根结点构建决策树
\[\begin{aligned}
Gain(D,色泽)=0.2756 \ Gain(D,根蒂)=0.1145 \ Gain(D,敲声)=0.2346 \\
Gain(D,纹理)=0.2346 \ Gain(D,脐部)=0.2756 \ Gain(D,触感)=0\end{aligned}
\]
比较六个属性的信息增益大小,选择脐部作为根结点
则数据集被划分为
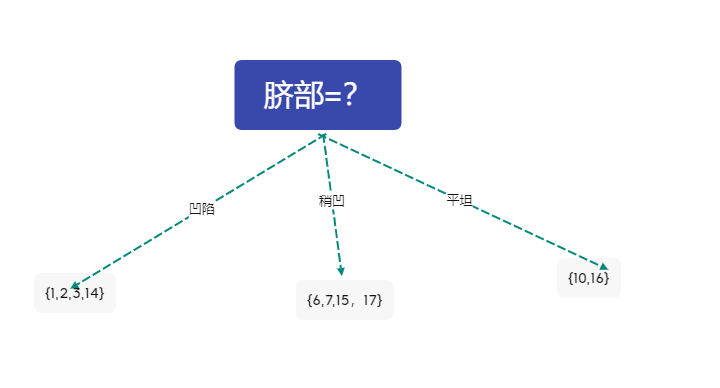
2 对分支结点\({1,2,3,14}\)进行划分
色泽 信息增益
根据色泽划分为 青绿,乌黑,浅白 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{0}{2} log_2 \frac{0}{2}+\frac{2}{2} log_2 \frac{2}{2})=0 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,色泽)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{1}{4}\times 0+\frac{2}{4} \times 0 +\frac{1}{4}\times 0) \\
&= 0.811\end{aligned}
\]
根蒂 信息增益
根据根蒂划分为 蜷缩 稍蜷 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{3} log_2 \frac{0}{3}+\frac{3}{3} log_2 \frac{3}{3})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})= 0.811\\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{3}{4}\times 0 +\frac{1}{4} \times 0) \\
&= 0.811\end{aligned}
\]
敲声 信息增益
根据色泽划分为 浊响,沉闷 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{2} log_2 \frac{0}{2}+\frac{2}{2} log_2 \frac{2}{2})=0 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{2}{4}\times 0 +\frac{2}{4} \times 1 ) \\
&=0.311\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{3} log_2 \frac{0}{3}+\frac{3}{3} log_2 \frac{3}{3})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{3}{4}\times 0+\frac{1}{4} \times 0 ) \\
&= 0.811\end{aligned}
\]
触感 信息增益
根据触感划分为 硬滑 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})= 0.811 \\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{4}{4}\times 0.811 ) \\
&= 0\end{aligned}
\]
选择分类结点构建决策树
\[\begin{aligned}
Gain(D,色泽)=0.811 \ Gain(D,根蒂)=0.811 \ Gain(D,敲声)=0.311 \\
Gain(D,纹理)=0.811 \ \ \ Gain(D,触感)=0\end{aligned}
\]
不妨选择色泽作为分类依据
形成的决策树
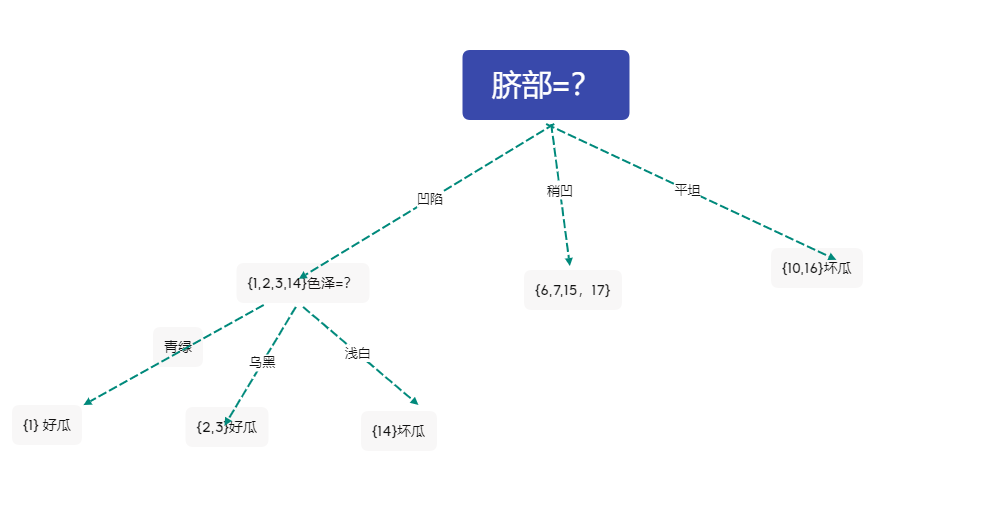
3 对分支 \({6,7,15,17}\)进行划分
色泽 信息增益
根据色泽划分为 青绿,乌黑 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{0}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})= 1 \\
Gani(D,色泽)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{2}{4}\times 1+\frac{2}{4} \times 1 ) \\
&= 0\end{aligned}
\]
根蒂 信息增益
根据根蒂划分为 蜷缩 稍蜷 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0。918\\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})= 1\\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{3}{4}\times 0.918 +\frac{1}{4} \times 0) \\
&= 0.3115\end{aligned}
\]
敲声 信息增益
根据色泽划分为 浊响,沉闷 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})= 0 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{3}{4}\times 0.918 +\frac{1}{4} \times 0 ) \\
&=0.3115\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{2}{4}\times 1+\frac{2}{4} \times 1 ) \\
&= 0\end{aligned}
\]
触感 信息增益
根据触感划分为 硬滑,软粘 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{3}{4}\times 0.918+\frac{1}{4} \times 0 ) \\
&= 0.2295\end{aligned}
\]
选择分类结点构建决策树
\[\begin{aligned}
Gain(D,色泽)=0 \ Gain(D,根蒂)=0.3115 \ Gain(D,敲声)=0.3115 \\
Gain(D,纹理)=0 \ \ \ Gain(D,触感)=0.2295\end{aligned}
\]
不妨选择根蒂作为分类依据
此时决策树为
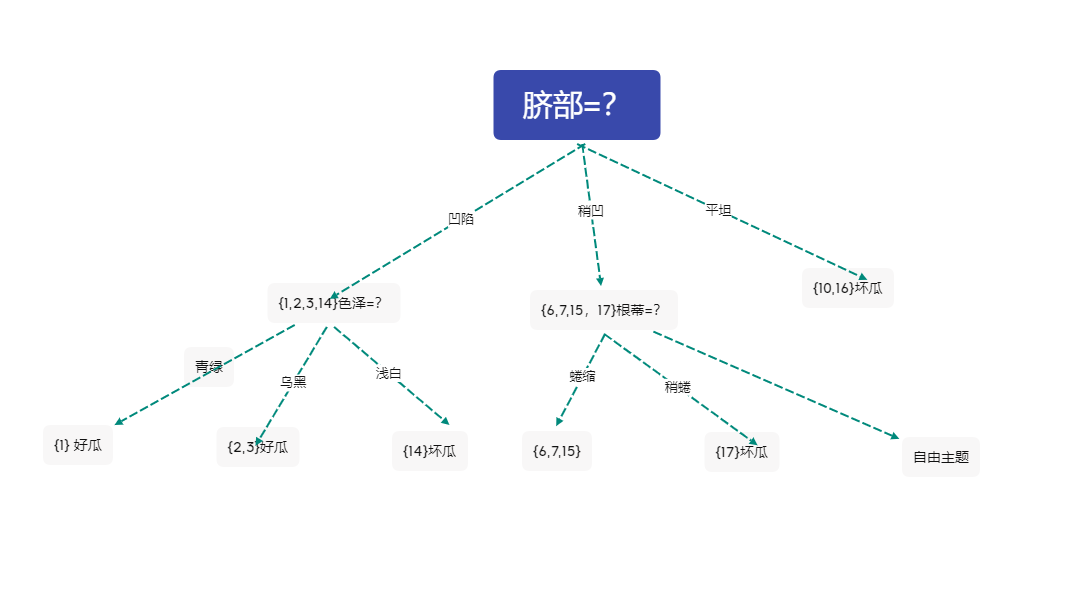
4 对分支\({6,7,15}\)进行划分
色泽 信息增益
根据色泽划分为 青绿,乌黑 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})= 0.918 \\
Gani(D,色泽)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 - (\frac{1}{3}\times 0+\frac{2}{3} \times 1 ) \\
&= 0.252\end{aligned}
\]
敲声 信息增益
根据色泽划分为 浊响 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\Ent(D)&= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 - (\frac{3}{3}\times 0.918 ) \\
&=0\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0\\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 - (\frac{2}{3}\times 1+\frac{1}{3} \times 0 ) \\
&= 0.252\end{aligned}
\]
触感 信息增益
根据触感划分为 软粘 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918\\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 - (\frac{3}{3}\times 0.918 ) \\
&= 0\end{aligned}
\]
选择分类结点构建决策树
\[\begin{aligned}
Gain(D,色泽)=0 .252 \ \ Gain(D,敲声)=0 \\
Gain(D,纹理)=0.252 \ \ \ Gain(D,触感)=0\end{aligned}
\]
不妨选择色泽作为分类依据
此时决策树为
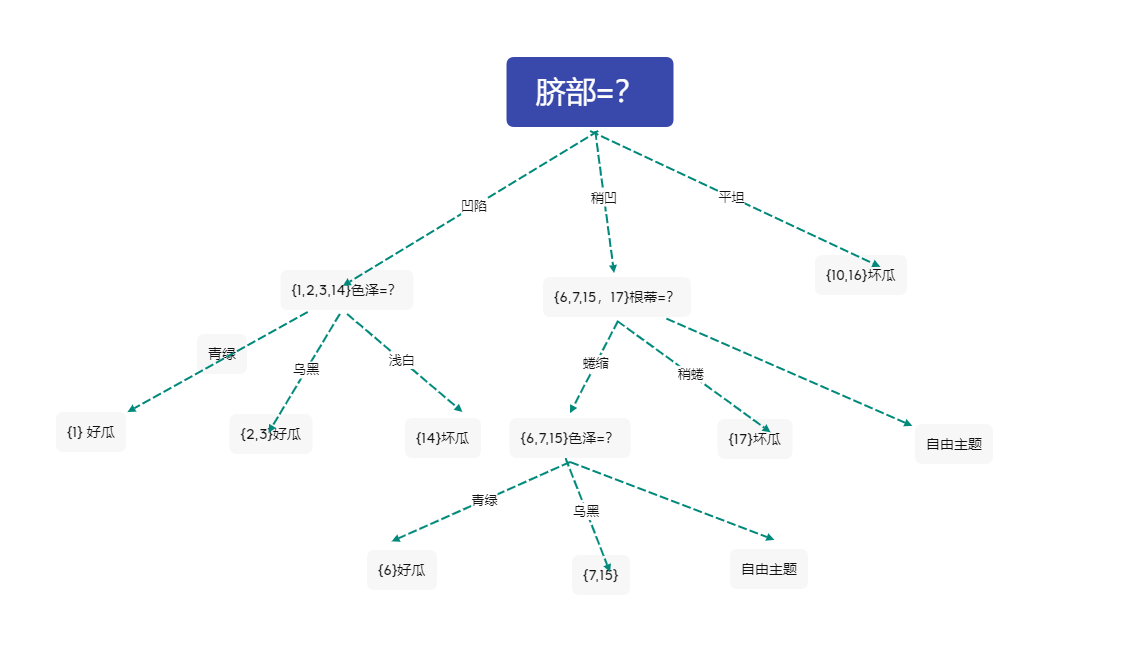
5 对分支\({7,15}\)进行划分
敲声 信息增益
根据色泽划分为 浊响 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1\\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{2}{2}\times 0.918 ) \\
&= 0\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0\\Ent(D)&= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{1}{2}\times 0+\frac{1}{2} \times 0 ) \\
&= 1\end{aligned}
\]
触感 信息增益
根据触感划分为 软粘 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1\\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{2}{2}\times 0.918 ) \\
&= 0\end{aligned}
\]
选择分类结点构建决策树
\[\begin{aligned}
\ \ Gain(D,敲声)=0 \ Gain(D,纹理)=1 \ \ \ Gain(D,触感)=0\end{aligned}
\]
选择纹理作为分类依据
此时决策树为
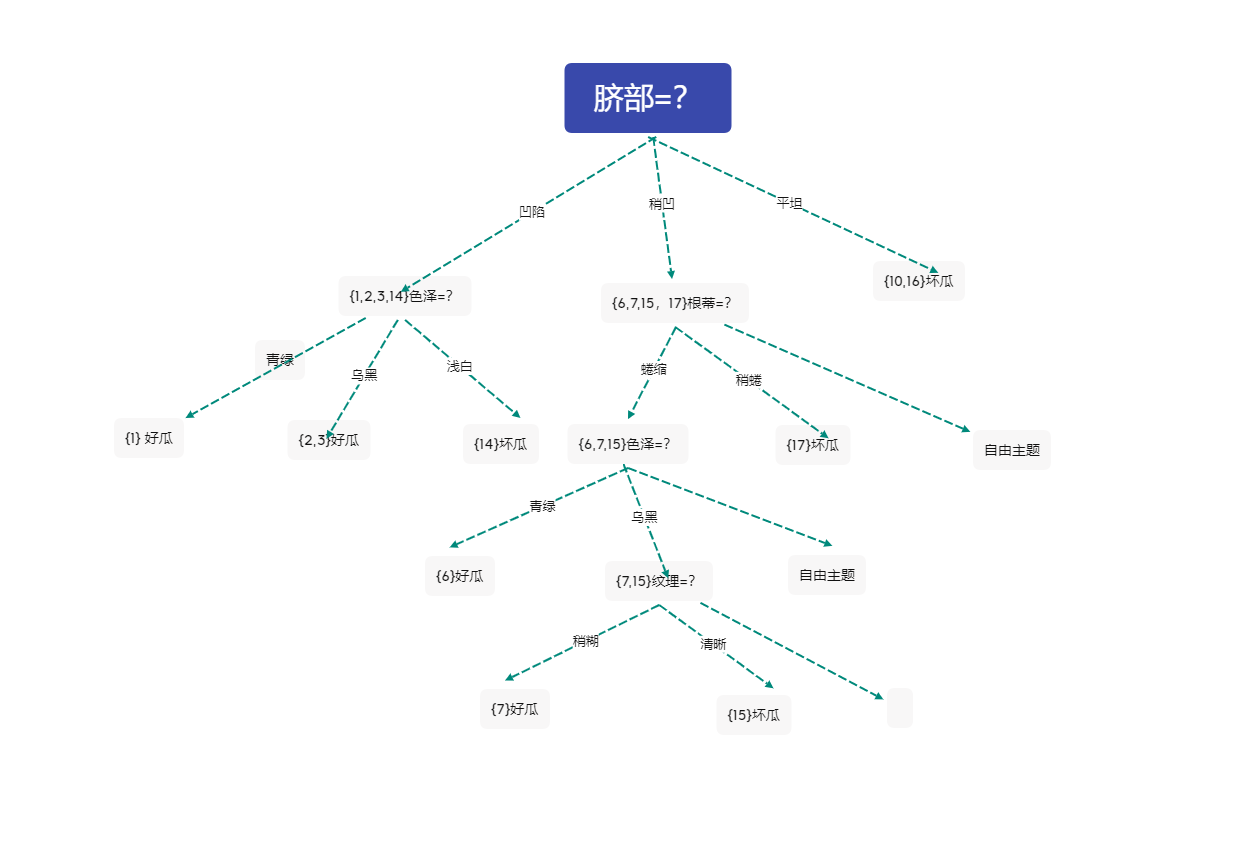
2 决策树后剪枝
1 考虑结点\(7,15\)
原分支(剪枝前),有三个样本被正确分类 验证集精度为 42.8%
剪枝后的决策树
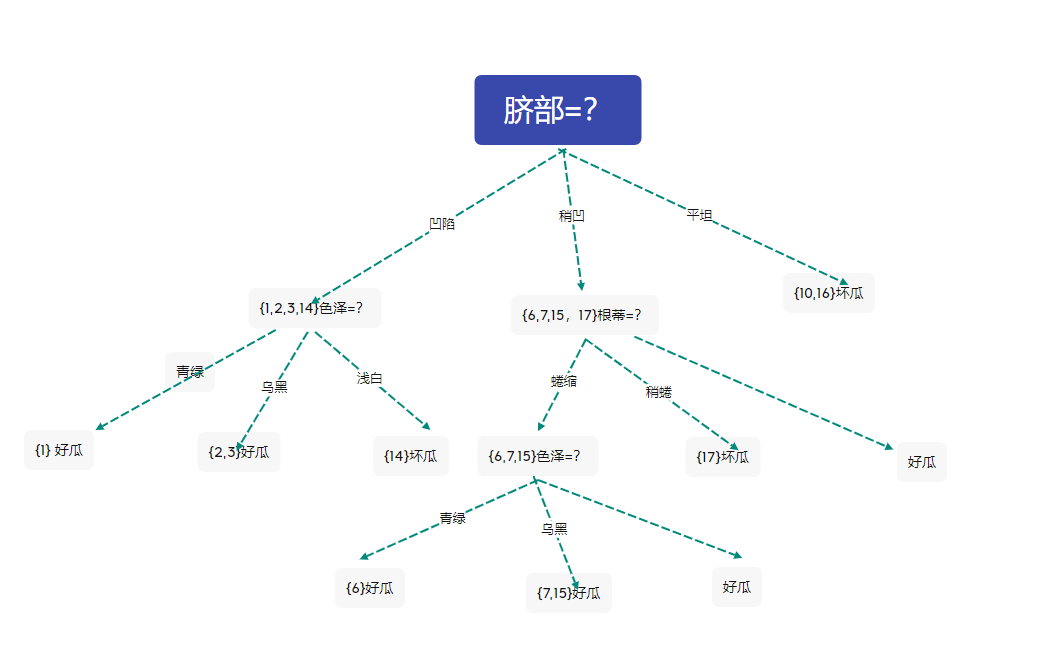
此时验证集有四个样本被正确分类,精度为57.1%
于是后剪枝策略决定剪枝,得到上图的决策树
2 考虑结点\(6,715\)色泽=?
由上图,决策树精度为57.1%
剪去结点后的决策树为
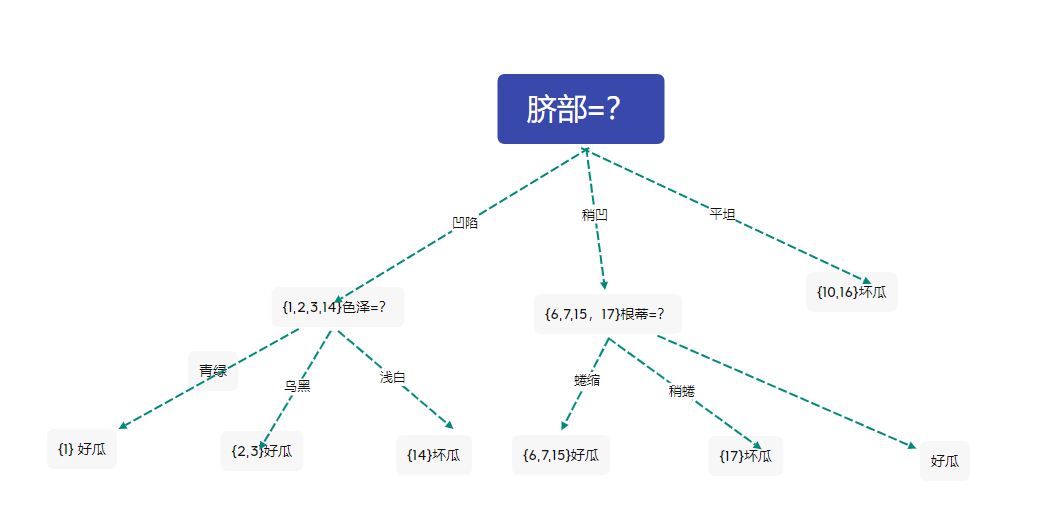
此时验证集有四个样本被正确分类,精度为57.1%
与未剪枝时的精度相同,西瓜书中采用了不剪枝的策略。在这里我们不妨采用剪枝的策略,于是得到上图的决策树
3 考虑结点\(1,2,3,14\)色泽=?
在上图基础上来考虑剪去结点\(1,2,3,14\)色泽=? ,剪枝后的决策树为
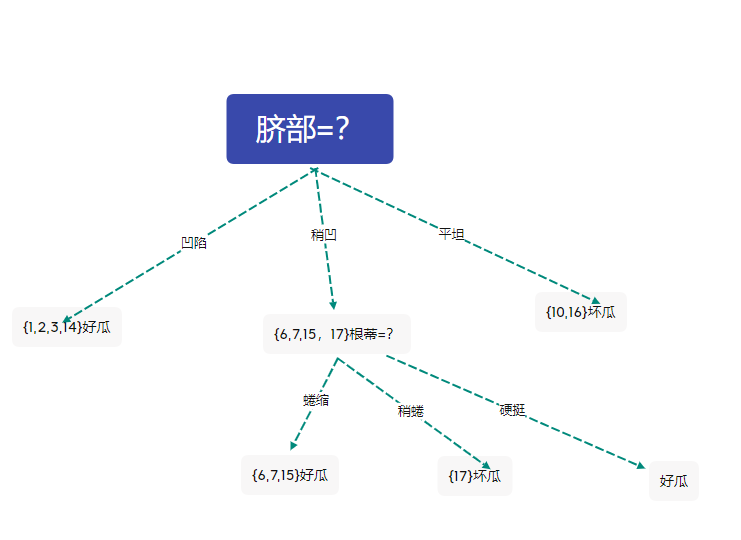
此时的决策树正确分类的样本5个,精度为71.4%
根据后剪枝策略,进行剪枝,得到上图的决策树
4考虑 \(6,7,15,17\)根蒂=?
剪枝后的决策树为
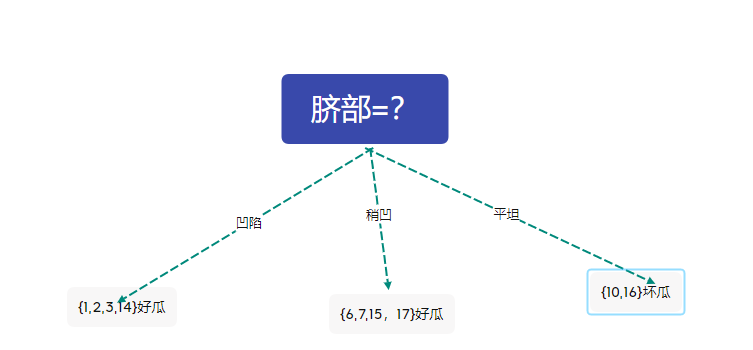
此时的决策树的精度仍然为71.4%
与未剪枝时的精度相同,西瓜书中采用了不剪枝的策略。在这里我们不妨采用剪枝的策略,于是得到上图的决策树
最终得到上图的决策树
决策树 机器学习,西瓜书p80 表4.2 使用信息增益生成决策树及后剪枝的更多相关文章
- 周志华-机器学习西瓜书-第三章习题3.5 LDA
本文为周志华机器学习西瓜书第三章课后习题3.5答案,编程实现线性判别分析LDA,数据集为书本第89页的数据 首先介绍LDA算法流程: LDA的一个手工计算数学实例: 课后习题的代码: # coding ...
- python实现简单决策树(信息增益)——基于周志华的西瓜书数据
数据集如下: 色泽 根蒂 敲声 纹理 脐部 触感 好瓜 青绿 蜷缩 浊响 清晰 凹陷 硬滑 是 乌黑 蜷缩 沉闷 清晰 凹陷 硬滑 是 乌黑 蜷缩 浊响 清晰 凹陷 硬滑 是 青绿 蜷缩 沉闷 清晰 ...
- 决策树ID3原理及R语言python代码实现(西瓜书)
决策树ID3原理及R语言python代码实现(西瓜书) 摘要: 决策树是机器学习中一种非常常见的分类与回归方法,可以认为是if-else结构的规则.分类决策树是由节点和有向边组成的树形结构,节点表示特 ...
- (二)《机器学习》(周志华)第4章 决策树 笔记 理论及实现——“西瓜树”——CART决策树
CART决策树 (一)<机器学习>(周志华)第4章 决策树 笔记 理论及实现——“西瓜树” 参照上一篇ID3算法实现的决策树(点击上面链接直达),进一步实现CART决策树. 其实只需要改动 ...
- LASSO回归与L1正则化 西瓜书
LASSO回归与L1正则化 西瓜书 2018年04月23日 19:29:57 BIT_666 阅读数 2968更多 分类专栏: 机器学习 机器学习数学原理 西瓜书 版权声明:本文为博主原创文章,遵 ...
- 朴素贝叶斯python代码实现(西瓜书)
朴素贝叶斯python代码实现(西瓜书) 摘要: 朴素贝叶斯也是机器学习中一种非常常见的分类方法,对于二分类问题,并且数据集特征为离散型属性的时候, 使用起来非常的方便.原理简单,训练效率高,拟合效果 ...
- 手把手生成决策树(dicision tree)
手把手生成决策树(dicision tree) 标签: Python 机器学习 主要參考资料: Peter HARRINGTON.机器学习实战[M].李锐,李鹏,曲亚东,王斌译.北京:人民邮电出版社, ...
- GZFramwork数据库层《二》单据表增删改查(自动生成单据号码)
运行效果: 使用代码生成器(GZCodeGenerate)生成tb_EmpLeave的Model 生成器源代码下载地址: https://github.com/GarsonZhang/GZCodeGe ...
- Javascript_06_表单验证(离开单项,输入框后提示信息)
Javascript_06_ 表单验证(离开单项,输入框后提示信息) 说明:对于必须输入的入力框,光标离开(使用 onblur方法)时进行检查.假如有错,红色的提示信息直接在该画面的这个输入框的后面显 ...
随机推荐
- go语言游戏服务端开发(二)——网络通信
一.网络层 网络游戏客户端除了全局登录使用http请求外,一般通过socket长连接与服务端保持连接.go语言的net包提供网络socket长连接相关操作. 对于服务端,一般经历 Listen.Acc ...
- Expression 表达式动态生成
http://blog.csdn.net/duan1311/article/details/51769119 以上是拼装和调用GroupBy的方法,是不是很简单,只要传入分组列与合计列就OK了! 下面 ...
- PHP垃圾回收机制的一些浅薄理解
相信只要入门学习过一点开发的同学都知道,不管任何编程语言,一个变量都会保存在内存中.其实,我们这些开发者就是在来回不停地操纵内存,相应地,我们如果一直增加新的变量,内存就会一直增加,如果没有一个好的机 ...
- Java面向对象系列(11)- instanceof和类型转换
instanceof 先看引用类型的类和instanceof比较的类有没有父子关系,有则可以编译,IDEA不报错 new一个对象,对象new所在的类和instanceof比较的类有没有父子关系,有则为 ...
- Python+Pygame开发太空大战/飞机大战完整游戏项目(附源代码)
项目名称:太空大战 开发环境:Python3.6.4 第三方库:Pygame1.9.6 代码编辑器:Sublime Text 先来看一下游戏画面吧! 游戏画面动态且丰富哦! 需求分析 利用Pyt ...
- 深入剖析 Laravel 服务容器
https://cloud.tencent.com/developer/article/1340400
- django错误处理
1.django.db.utils.OperationalError: no such table 意思:没有这个app应用对应的数据表的,可以用 python manage.py makemigra ...
- ARC122C-Calculator【乱搞,构造】
正题 题目链接:https://atcoder.jp/contests/arc122/tasks/arc122_c 题目大意 一个数对开始是\((0,0)\),每次可以选择一个数加一或者让一个数加上另 ...
- YbtOJ#912-神秘语言【结论,欧拉定理】
正题 题目链接:http://www.ybtoj.com.cn/problem/912 题目大意 给出\(L,R\),求有多少长度在\([L,R]\)之间的字符串满足依次取出所有偶数位置的放在最前面后 ...
- Python3入门系列之-----range和xrange的区别详解,你明白了吗?
前言 range()是Python的内置函数,用于创建整数的列表,可以生成递增或者递减的数列. xrange也有相同的功能, 今天来看下它们之间的不同. range 函数说明:range([start ...
