【AGC板刷记录】

这个帖子，是在自己学知识点累了的时候就看看$AGC$的题目来休息。

而且白天上课可以做（

AGC-001

$A\ BBQ Easy$

考虑从小到大排，相邻两个取为一对。

BBQ Easy

#include<iostream>

#include<cstdio>

#include<algorithm>

#define ll long long

#define N 100000

ll n;

ll num[N],ans;

int main(){

	scanf("%lld",&n);

	for(int i = 1;i <= 2 * n;++i)

	scanf("%lld",&num[i]);

	std::sort(num + 1,num + 2 * n + 1);

	for(int i = 2 * n - 1;i >= 1;i -= 2)

	ans += num[i];

	std::cout<<ans<<std::endl;

}

$B\ Mysterious Light$

光线实则是在平行四边形里游走的。

Mysterious Light

#include<cstdio>

#include<algorithm>

#define LL long long

using namespace std;

LL n,x,ans,x1,x2;

int main()

{

	scanf("%lld%lld",&n,&x);

	ans=n;

	x1=x,x2=n-x;

	while(1)

	{

		if(x1<x2) swap(x1,x2);

		if(!x2) break;

		if(x1%x2==0) ans-=x2;

		ans+=x2*(x1/x2)*2;

		x1-=x2*(x1/x2);

	}

	printf("%lld\n",ans);

}

$C\ Shorten Diameter$

考虑$n$很小，考虑枚举直径中间的那个点/边，以他为中间的树高不能超过$\frac{k}{2}$

暴力$dfs$就行了。

明天机房要封起来，什么体育机考。。。

明天安心卷文化课吧。

Shorten Diameter

#include<iostream>

#include<cstdio>

#define ll long long

#define N 40005

struct P{int fr,to,next;}e[N];

ll n,k,head[N],cnt;

inline void add(ll x,ll y){

	e[++cnt].to = y;

	e[cnt].fr = x;

	e[cnt].next = head[x];

	head[x] = cnt;

}

ll tot,ans;

inline void dfs(ll u,ll fa,ll st){

	tot ++ ;

	if(st == 0)

	return ;

	for(int i = head[u];i;i = e[i].next){

		int v = e[i].to;

		if(v == fa)

		continue;

		dfs(v,u,st - 1);

	}

}

int main(){

	scanf("%lld%lld",&n,&k);

	for(int i = 1;i <= n - 1;++i){

		ll x,y;

		scanf("%lld%lld",&x,&y);

		add(x,y);

		add(y,x);

	}

	if(k % 2 == 1){

		for(int i = 1;i <= cnt;++i){

			tot = 0;

			ll u = e[i].fr,v = e[i].to;

			dfs(u,v,k / 2);

			dfs(v,u,k / 2);

			ans = std::max(ans,tot);

		}

	}

	if(k % 2 == 0){

		for(int i = 1;i <= n;++i)

		tot = 0,dfs(i,0,k / 2),ans = std::max(ans,tot);;

	}

	std::cout<<n - ans<<std::endl;

}

$D\ Arrays and Palindrome$

回来了。

这题是看题解做的。

因为没有怎么看懂题目。

考虑把相等的点连上边，那么要求的是让所有点连上一起。

然后发现如果说出现一个长度为奇数的回文串，最中间的那个点就会没有线连，然后为了让它和其他的点连上，这个点的度数必须是1，然后为了保证一笔画，这样的点必须至多出现两个，所以奇数长度的回文串至多只能有两个，否则就无解了，然后多画几组会发现。。如果出现奇数长度的回文串它们还必须出现在一头一尾

那么就开始构造

那么剩下的就是构造啦

当全部都是偶数的时候，我们在最开头先放一个1，这样后面就错开了，然后第1到m−1都可以直接复制下来，至于最后一个回文串，我们可以放一堆2中间夹一个1这样（具体自己画一下就知道了）

当有一个奇数的时候，我们把它放在A的最后，B的前面部分的构造方式同上，最后一个长度为奇数的回文串就简单一些，直接全部上2就好了

当有两个奇数的时候，我们将其放在一头一尾，然后B的第一个元素设成$A1+1$，这样后面的情况就和只有一个奇数、并且已经放了一个1的情况一样了，剩下的构造同上

这些都其他人的题解，自己果真是不会做构造题的。

Arrays and Palindrome

#include<iostream>

#include<cstdio>

#include<cstring>

using namespace std;

const int N=1e5+10;

int a[N],b[N*2],lis[3];

int n,m,cnt;

bool firstcheck(){

	int cnt=0;

	for (int i=1;i<=n;++i)

		cnt+=a[i]&1;

	return cnt<=2;

}

void get_b(){

	int sum;

	if (cnt==0){

		b[++b[0]]=1; sum=m-1;

		for (int i=1;i<n;++i) b[++b[0]]=a[i],sum-=a[i];

		if (sum==0) return;

		sum-=1; sum/=2;

		for (int i=1;i<=sum/2;++i) b[++b[0]]=2;

		b[++b[0]]=1;

		for (int i=sum/2+1;i<=sum;++i) b[++b[0]]=2;

	}

	else if (cnt==1){

		b[++b[0]]=1;

		for (int i=1;i<n;++i) b[++b[0]]=a[i];

		for (int i=1;i<=(a[n]-1)/2;++i) b[++b[0]]=2;

	}

	else{

		b[++b[0]]=a[1]+1;

		for (int i=2;i<n;++i) b[++b[0]]=a[i];

		for (int i=1;i<=(a[n]-1)/2;++i) b[++b[0]]=2;

	}

}

int main(){

#ifndef ONLINE_JUDGE

	freopen("a.in","r",stdin);

#endif

	scanf("%d%d",&m,&n);

	for (int i=1;i<=n;++i) scanf("%d",a+i);

	if (!firstcheck()){printf("Impossible\n"); return 0;}

	cnt=0;

	for (int i=1;i<=n;++i){

		if ((a[i]&1))

			lis[++cnt]=i;

	}

	if (lis[1]) swap(a[n],a[lis[1]]);

	if (lis[2]) swap(a[1],a[lis[2]]);

	for (int i=1;i<=n;++i) printf("%d ",a[i]); printf("\n");

	get_b();

	printf("%d\n",b[0]);

	for (int i=1;i<=b[0];++i) printf("%d ",b[i]); printf("\n");

}

$E\ BBQ Hard$

考虑求这么一个柿子。

$\sum_i^n\sum_{j = i + 1}^n\binom{a_i + b_i + a_j + b_j}{a_i + a_j}$

好精妙的一个题目。发现虽然$n^2$不在我们的承受范围内，但是$A^2$在，看到这种特殊的数据范围，我们应该保持敏感。

我们考虑组合意义$\binom{a_i + b_i + a_j + b_j}{a_i + a_j}$为$(-a_i,-b_i)$到$(a_j,b_j)$的方案数。

考虑直接$dp$求得。

然后变形柿子，

$Ans = \frac{1}{2}(\sum_i^n\sum_{j}^n\binom{a_i + b_i + a_j + b_j}{a_i + a_j} - \binom{a_i + b_i + a_i + b_i}{a_i + a_i})$

BBQHard

#include<iostream>

#include<cstdio>

#define ll long long

#define N 2005

#define mod 1000000007

ll f[2 * N + 5][2 * N + 5],a[N * 100],b[N * 100],s[4 * N + 5],inv[4 * N + 5];

ll n;

inline ll C(ll a,ll b){return (s[a] * inv[b] % mod * inv[a - b] % mod) % mod;}

inline ll pow(ll a,ll b){

	ll ans = 1;

	while(b){

		if(b & 1)

		ans = a * ans % mod;

		a = a * a % mod;

		b >>= 1;

	}

	return ans;

}

ll ans = 0;

int main(){

	scanf("%lld",&n);

	for(int i = 1;i <= n;++i)

	scanf("%lld%lld",&a[i],&b[i]),f[N - a[i]][N - b[i]] ++ ;

	for(int i = 1;i <= 2 * N;++i)

	for(int j = 1;j <= 2 * N;++j)

	f[i][j] = (f[i - 1][j] + f[i][j - 1] + f[i][j]) % mod;

	s[0] = 1;

	for(int i = 1;i <= 4 * N;++i)

	s[i] = (s[i - 1] * i) % mod;

	inv[4 * N] = pow(s[4 * N],mod - 2);

	for(int i = 4 * N - 1;i >= 1;--i)

	inv[i] = (inv[i + 1] * (i + 1)) % mod;

	for(int i = 1;i <= n;++i)

	ans = (ans + f[N + a[i]][N + b[i]] - C(a[i] + a[i] + b[i] + b[i],a[i] + a[i]) + mod) % mod;

	std::cout<<(ans * inv[2] % mod)%mod<<std::endl;

}

$F\ Wide Swap$

不太会做的。

题解都看了挺久的。

考虑先把这个序列变换一下成为$Q$

使$Q_{p_i} = i$

那么也是尽量让$Q$的排列更小。

那么对于一个$Q_i - Q_j$的绝对值小于$k$的数值$Q_i,Q_j$其相对位置是不变的。

这个大小关系具有传递性，所以一个点只要向他的边界连边就行了。

然后拓扑序列一下就好了（注意要把所有边反向，然后拓扑排序（也就是倒着拓扑排序），但每次优先取编号最大的点，拓扑编号也从 N 往 1 编号）。

代码鸽了。

（总算是写完一套$AGC$了，感觉没几题会做的。继续努力吧）

AGC-002

$A$

直接考虑判断。

代码不放了。

$B\ Box and Ball$

考虑维护这些东西，每个盒子的大小:now[x],以及当前是否有可能有红球may[x]

直接模拟维护就好，最后统计答案。

Box and Ball

#include<iostream>

#include<cstdio>

#define ll long long

#define N 100005

ll n,m,now[N];

bool may[N],out[N];

int main(){

	scanf("%lld%lld",&n,&m);

	may[1] = 1;

	for(int i = 1;i <= n;++i)

	now[i] = 1;

	for(int i = 1;i <= m;++i){

		ll x,y;

		scanf("%lld%lld",&x,&y);

		if(now[x]){

			if(may[x]){

			may[y] = may[x];

		}

		now[x] -- ,now[y] ++ ;

		if(!now[x])

		may[x] = 0;

		}

	}

	ll ans = 0;

	for(int i = 1;i <= n;++i)

	if(may[i])

	ans ++ ;

	std::cout<<ans<<std::endl;

}

[AGC002C] Knot Puzzle

这题写了个不知名贪心。

正确性确实会证。

但是没过。。。

所以先鸽着。

[AGC002E] Candy Piles

开始觉得是对抗搜索，后来觉得是博弈论推结论，后来发现是神仙题。

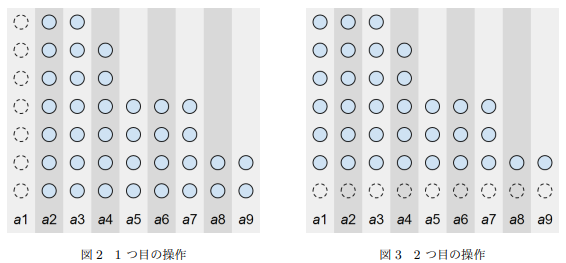
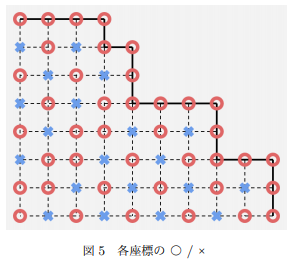
考虑先把所有的数都排序，那么每次的操作就是把左边一列删除，或者把下面一行删除，那么很轻松的就能求出

观察性质，则有在对角线上的颜色都是一样的，且同一列和同一行的颜色交替出现，那么判断一下(0,0)是不是必胜点就行了。

[AGC002E] Candy Piles

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

template <class T>

inline void read(T &x) {

    x = 0;

    char c = getchar();

    bool f = 0;

    for (; !isdigit(c); c = getchar()) f ^= c == '-';

    for (; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);

    x = f ? -x : x;

}

template <class T>

inline void write(T x) {

    if (x < 0) {

        putchar('-');

        x = -x;

    }

    T y = 1;

    int len = 1;

    for (; y <= x / 10; y *= 10) ++len;

    for (; len; --len, x %= y, y /= 10) putchar(x / y + 48);

}

const int MAXN = 1e5;

int n, a[MAXN + 5];

int main() {

    read(n);

    for (int i = 1; i <= n; ++i) read(a[i]);

    sort(a + 1, a + n + 1, greater<int>());

    for (int i = 1; i <= n; ++i)

        if (i + 1 > a[i + 1]) {//找到以原点为左下角的最大正方形，其右上方顶点为 (i, i)

            int j = 0;

            for (; a[j + i + 1] == i; ++j);

            if (((a[i] - i) & 1) || (j & 1)) puts("First");

            else puts("Second");

            break;

        }

    return 0;

}

这题之后可能会另开一个博客。感觉全写在这里有点乱