Asia-Dhaka 2017

Asia-Dhaka 2017

A - Brick Walls

题目描述：如下图，编坐标与路径，给出两个坐标，问两个坐标的最短距离是多少。

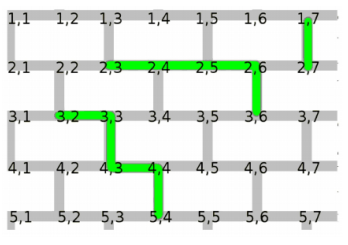
solution
先阶梯型地走，然后注意“中”字走法。

时间复杂度：\(O(1)\)(每次询问)

B - Bracket Sequence

题目描述：有一个括号序列，该括号序列有四种括号，问以位置\(i\)开头的合法括号序列最长有多长。

solution
首先匹配好括号，然后将相邻的合法括号序列处理一下即可。

时间复杂度：\(O(n)\)

C - Making a Team

题目描述：有\(n\)个人，从中选择\(m\)个人组成一队，队中有四个职位，每个职位选择一个人担任，但一个人可以有很多职位，问有多少种组队方案。

solution
分类讨论：

1. 从\(n\)个人中选一个人担任四个职位，其他人可选可不选。
2. 从\(n\)个人中选两个人担任四个职位，其他人可选可不选。
3. 从\(n\)个人中选三个人担任四个职位，其他人可选可不选。
4. 从\(n\)个人中选四个人担任四个职位，其他人可选可不选。

时间复杂度：\(O(1)\)

D - Christmas Tree

题目描述：给出一棵树（\(n\)个点），从树上删掉一些点（如果删去的点不是叶子节点，则删掉以该点为根的子树），使得每个点有\(m\)个儿子。问最终树上最多还有多少个点。

solution
树形dp。

时间复杂度：\(O(n)\)(每次询问)

E - Leap Birthdays

题目描述：给出一个人的出生年月日，问到某一年的最后一天为止，这个人过了多少次生日。

solution
模拟。

时间复杂度：\(O(1000)\)(每次询问)

F - Megamind

题目描述：有个人用一支枪去打怪，怪物一开始有\(E\)生命值，枪有\(K\)发子弹，每颗子弹可造成\(P\)点伤害，当\(K\)发子弹打完后，需要时间装子弹，在这段时间怪物会恢复\(R\)生命值。问至少需要多少枪才能打死这个怪物，或者永远打不死。

solution
简单数学。

时间复杂度：\(O(1)\)(每次询问)

G - XOR Path

题目描述：给出一棵树，树边有权值，一条路径的值为路径的边的权值的异或和。输出路径的值为\(0\)~\(2^{16}-1\)每个数对应的路径数。

solution
根据\(XOR\)的性质，两点形成路径的值可以看做这两点到根的路径的值的异或和。然后问题就转化为类似FFT的问题，用快速沃尔什变换解决。

时间复杂度：\(O(nlogn)\)

H - Angry Birds Transformers

题目描述：二维平面第一象限上有一些点，有一个人沿着\(x\)轴正向移动，他的视角范围为\(90^{\circ}\)，视角范围关于\(x=p\)对称(\(p\)为他走到的位置)。问他最多能同时看到多少个点。

solution
将点映射到\(x\)轴上(开始看到该点的位置以及最后看到该点的位置)，然后求个前缀和的最大值即可。

时间复杂度：\(O(n)\)

I - Divisors

题目描述：设\(d(n)\)表示\(n\)的约数个数，\(AF(n)=\prod_{i=1}^{n} i!\)，求\(d(AF(n))\)

solution
\(AF(n)=\prod_{i=1}^{n} i!=\prod_{i=1}^{n} i^{n-i+1}\)
枚举质因数\(d\)，\(d\)的指数\(i\)，现要算出\(AF(n)\)有多少质因数\(d\)
设\(d^i\)的倍数有\(x\)个，\(x=\frac{n}{d^i}\)
\(s_d=\sum_{i=0} (n-d^i+1)x+\frac{x(x-1)}{2} d^i\)
答案就是\(\prod (s_d+1)\)

时间复杂度：\(O(\sigma(n)logn)\)(每次询问)

J - Substring Sorting

题目描述：给出一个字符串，询问长度为\(K\)的子串按字典序排好后（并去重，只保留位置较前的），排名为\(M\)的字符串的第一个字符的位置。

solution
后缀数组+线段树，但去重的问题还没解决（不会只保留位置较前的）

时间复杂度：\(O(nlogn)\)

K - Bermuda Polygon

solution
听说是半球上凸包。