hdu 6038 Function

Function

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 1025    Accepted Submission(s): 457

Problem Description

You are given a permutation a from 0 to n−1 and a permutation b from 0 to m−1.

Define that the domain of function f is the set of integers from 0 to n−1, and the range of it is the set of integers from 0 to m−1.

Please calculate the quantity of different functions f satisfying that f(i)=bf(ai) for each i from 0 to n−1.

Two functions are different if and only if there exists at least one integer from 0 to n−1 mapped into different integers in these two functions.

The answer may be too large, so please output it in modulo 109+7.

 

Input

The input contains multiple test cases.

For each case:

The first line contains two numbers n, m. (1≤n≤100000,1≤m≤100000)

The second line contains n numbers, ranged from 0 to n−1, the i-th number of which represents ai−1.

The third line contains m numbers, ranged from 0 to m−1, the i-th number of which represents bi−1.

It is guaranteed that ∑n≤106, ∑m≤106.

 

Output

For each test case, output "Case #x: y" in one line (without quotes), where x indicates the case number starting from 1 and y denotes the answer of corresponding case.

 

Sample Input

3 2

1 0 2

0 1

3 4

2 0 1

0 2 3 1

 

Sample Output

Case #1: 4

Case #2: 4

 

Source

2017 Multi-University Training Contest - Team 1

 

Recommend

liuyiding   |   We have carefully selected several similar problems for you:  6044 6043 6042 6041 6040 

题意：
给出两个序列，一个是0~n-1的排列a，另一个是0~m-1的排列b，现在求满足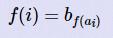的f的个数。

思路：

找到a序列中的循环节个数，并且记录每个循环节中有多少因子，b序列同理

如果a中的某个循环节里面因子的个数能整除 b中某个循环节的因子个数，那就加上b的这个循环节因子的个数

最后乘起来就是结果，

然而一脸懵逼，传说中的高等线代。。。。。

#include <iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<bits/stdc++.h>

using namespace std;
const long long mod=1e9+;
int n,m;
int a[],b[],a1[],b1[];
bool vis[];
int acir,bcir;
int main()
{
    int cas=;
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=;i<n;i++) scanf("%d",&a[i]);
        for(int i=;i<m;i++) scanf("%d",&b[i]);
        memset(vis,,sizeof(vis));
        acir=;
        for(int i=;i<n;i++)
        {
            if (vis[i]) continue;
            int k=i;
            acir++; a1[acir]=;
            while(!vis[k])
            {
                vis[k]=;
                a1[acir]++;
                k=a[k];
            }
        }
        bcir=;
        memset(vis,,sizeof(vis));
        for(int i=;i<m;i++)
        {
            if (vis[i]) continue;
            int k=i;
            bcir++; b1[bcir]=;
            while(!vis[k])
            {
                vis[k]=;
                b1[bcir]++;
                k=b[k];
            }
        }
       long long ans=;
       for(int i=;i<=acir;i++)
       {
           long long tmp=;
           for(int j=;j<=bcir;j++)
               if (a1[i]%b1[j]==) tmp+=b1[j];
           ans=ans*tmp%mod;
       }
       printf("Case #%d: %lld\n",++cas,ans%mod);
    }
    return ;
}