SPSS t 检验

在针对连续变量的统计推断方法中，最常用的是 t 检验和方差分析两种。

t 检验，又称 student t 检验，主要用于样本含量较小（例如n<30），总体标准差未知的正态分布资料。它是用 t 分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显著。

u 检验适用于总体标准差已知的小样本均数的假设检验，或总体标准差未知的大样本均数的假设检验。当样本数较大时，t 检验和 u 检验可以等同使用。

t 检验又三种：

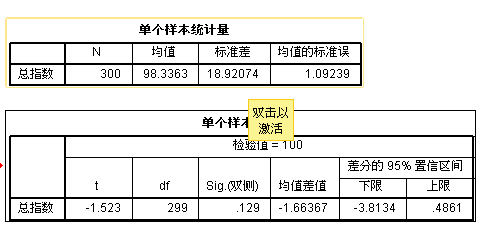
（1）单样本 t 检验过程：进行样本均数与已知总体均数的比较。

当样本量足够大，即使原数据不服从正态分布，由中心极限定理可知，其样本均数的抽样分布仍然是正态的。因此当样本量较大时，研究者很少去考虑单样本 t 检验的适用条件，此时真正会限制该方法使用的是均数是否能够代表相应数据的集中趋势，只要数据分布不是强烈的偏态，一般而言单样本 t 检验都是适用的。

当样本例数 n 较小时，一般要求样本取自正态总体，可以通过K-S检验来考察，该方法适用于大样本，也可以用更直观的作图方法判断，一般而言，单样本 t 检验是一个非常稳健的统计方法，只要没有明显的极端值，其分析结果都是稳定的。

（2）独立样本 t 检验过程：进行两样本均数差别的比较，即通常所说的两组资料的 t 检验。

进行两样本均数比较的 t 检验要求两样本来自的总体方差相等，即方差齐性。

当两样本所在总体的方差不同时，需要对结果进行一定的校正，再按相应的 t 值和自由度计算出相对应的 P 值，就是所谓的方差不齐时用于比较两个样本的 t’ 检验。

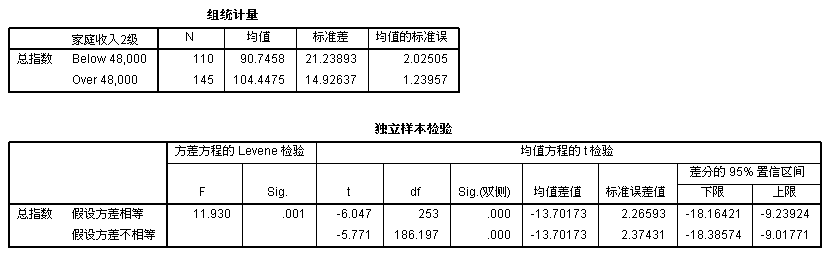
下图是参考资料1中比较高收入家庭和低收入家庭的消费者信心平均水平。

在应用 t 检验进行两样本均数的比较时，要求数据满足以下3个条件。

a、独立性，各观察值之间是相互独立的，不能相互影响。在实际应用中，独立性对结果影响较大，但检验数据独立性的方法比较复杂，一般都是根据资料的性质来判断。

b、正态性，各个样本均来自正态分布的总体。t 检验对资料的正态性有一定的耐受能力，如果资料只是稍微偏离正态，结果仍然是稳定的。

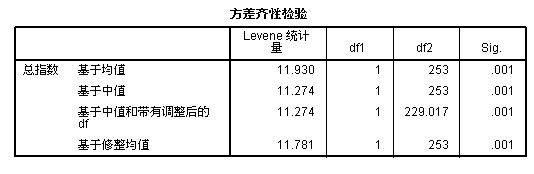
c、方差齐性，各个样本所在总体的方差相等。这个对结论影响较大，在进行均数比较时方差齐性检验更为重要。可通过Levene's 检验来进行。

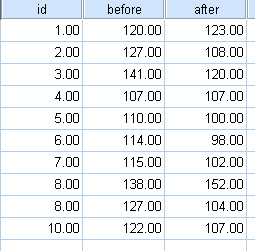
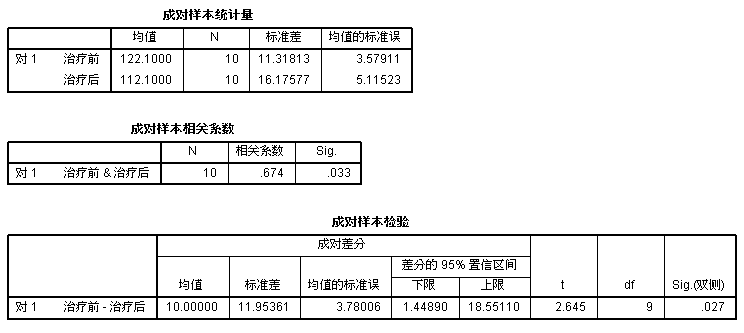
（3）配对样本 t 检验过程：进行配对资料的均数比较，即配对 t 检验。

在很多科学研究中，常采用配对设计来提高研究效率，常见的配对设计有4种情况：a、同一受试对象处理前后的数据；b、同一受试对象两个部位的数据；c、同一样品用两种方法检验的结果；d、配对的两个受试对象分别接受两种处理后的数据。在进行配对设计得到的样本数据中，每对数据之间都有一定的相关，如果忽略这种关系就会浪费大量的统计信息。

配对 t 检验的基本原理是为每对数据求差值，如果两种处理实际上没有差异，则差值的总体均数应当为0，从该总体中抽出的样本其均数也应当在0附近波动；反之，如果两种处理有差异，差值的总体均数应当远离0，其样本均数也应当远离0。这样，通过检验该差值总体均数是否为0，就可以得知两种处理有无差异。

配对样本 t 检验过程的功能实际上是和单样本 t 检验过程相重复的（等价于已知总体均数为0的情况），但配对样本 t 检验过程使用的数据输入格式和前者不同，因此它仍有存在价值。

由于配对 t 检验的本质就是单样本 t 检验，因此其适用条件的考察也和单样本 t 检验近似。

参考资料：

1. 张文彤. 《SPSS统计分析基础教程》