[CSP-S模拟测试]:光线追踪（线段树）

题目背景

　　初中时的乔猫试着组建了$NEWorld$开发组，可是不久之后却因为合作上的问题（和乔猫工程水平差，代码混乱的问题），开发组成员之间常常产生矛盾，关系越来越不如以前......一年下来，受到长期挫折的乔猫最终放弃了$NEWorld$，决定在信息竞赛方面努力奋斗......
　　是一年过去，上了高中的乔猫突发奇想，决定自己尝试写一个基于八叉树$BVH$（空间细分）的光线追踪渲染器。为了向自己的中二时代致敬，渲染的模型也是一个“方块组成的世界”......同样，为了简化，这里只考虑二维的情况......（貌似简化太多了吧$233$）

---

题目描述

　　考虑一个二维平面，摄像机在$(0,0)$的位置，初始时平面上没有障碍物。现在执行$Q$次操作，操作有两种（假设这是第$i$次操作，$1\leqslant i\leqslant Q$）：
　　$1.$给定$x_0,y_0,x_1,y_1(x_0<x_1,y_0<y_1)$，创建一个每条边与坐标轴平行的长方形障碍物，包含所有满足$x_0\leqslant x\leqslant x_1$且$y_0\leqslant y\leqslant y_1$的点$(x,y)$（如果这个区域的某一部分已经存在障碍，则直接覆盖掉它，具体请看样例）。这个障碍物的编号为$i$。
　　$2.$给定向量$(x,y)$，会有一个动点从摄像机所在的$(0,0)$位置出发，以$(x,y)$所指的方向前进，直到碰到第一个障碍物为止。
　　对于第$2$种操作，输出最先碰到的障碍物的编号。若不会碰到任何障碍物，输出$0$。

---

输入格式

　　输入文件名为$raytracing.in$。
　　输入文件第一行一个正整数$Q$，表示操作总数。
　　接下来的$Q$行，每行第一个正整数$op_i$为操作种类（保证为$1$或$2$）。如果为$1$，则接下来四个正整数$x_0,y_0,x_1,y_1(x_0<x_1,y_0<y_1)$表示障碍的位置；如果为 $2$，则接下来两个正整数$x,y$表示前进方向。

---

输出格式

　　输出文件名为$raytracing.out$。
　　输出文件包含$R$行（$R$为第$2$种操作的总数），每行一个正整数，表示第一个碰到的障碍物编号。

---

样例

样例输入：

10
1 3 3 10 4
1 4 2 5 6
2 6 2
1 2 8 4 10
1 0 6 3 9
2 5 2
2 8 6
2 2 9
2 4 7
1 5 7 10 10

样例输出：

1
2
2
5
0

---

数据范围与提示

样例解释：

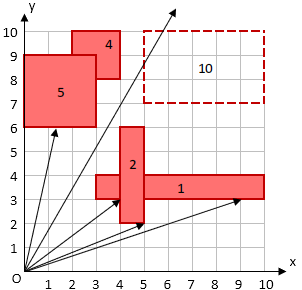
　　在$9$次操作之后，平面的一部分如图所示（箭头为所有第$2$种操作询问的路线）。

数据范围：

　　对于$30\%$的数据：$Q\leqslant 1,000$。
　　对于另外$30\%$的数据：$0\leqslant x_0,y_0,x_1,y_1,x,y\leqslant 200$。
　　对于$100\%$的数据：$Q\leqslant 10^5,0\leqslant x_0,y_0,x_1,y_1,x,y\leqslant 10^9,x_0<x_1,y_0<y_1;x_0$和$y_0$不全为$0$，$x$和$y$不全为$0$。

---

题解

撞上无非就分两种情况：

　　$\alpha.$撞底下。

　　$\beta.$撞左边。

那么开两棵线段树分别维护最早的撞上的是哪个就好了。

注意斜率是$90$度的时候不要除$0$，还有如果同时撞上多个的话输出编号最大的就好了（我也不知道为什么额……）

时间复杂度：$\Theta(Q\log Q)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
#define L(x) x<<1
#define R(x) x<<1|1
using namespace std;
const double eps=-1e-5;
struct rec{int opt,x0,y0,x2,y2;}e[100001];
map<double,int> mp;
int Q;
int cnt,top;
pair<int,int> tr[400001][2],ansx,ansy;
double slope[300001];
double getslope(int x,int y){return x?(double)y/x:0x3f3f3f3f;}
void build(int x,int l,int r)
{
	tr[x][0].first=tr[x][1].first=0x3f3f3f3f;
	if(l==r)return;
	int mid=(l+r)>>1;
	build(L(x),l,mid);
	build(R(x),mid+1,r);
}
void add(int x,int l,int r,int L,int R,int w,int id,int p)
{
	if(r<L||R<l)return;
	if(L<=l&&r<=R){if(w<=tr[x][p].first)tr[x][p]=make_pair(w,id);return;}
	int mid=(l+r)>>1;
	add(L(x),l,mid,L,R,w,id,p);
	add(R(x),mid+1,r,L,R,w,id,p);
}
void ask(int x,int l,int r,int k)
{
	if(tr[x][0].first<ansx.first)ansx=tr[x][0];
	if(tr[x][0].first==ansx.first)ansx.second=max(ansx.second,tr[x][0].second);
	if(tr[x][1].first<ansy.first)ansy=tr[x][1];
	if(tr[x][1].first==ansy.first)ansy.second=max(ansy.second,tr[x][1].second);
	if(l==r)return;
	int mid=(l+r)>>1;
	if(k<=mid)ask(L(x),l,mid,k);
	else ask(R(x),mid+1,r,k);
}
int main()
{
	scanf("%d",&Q);
	for(int i=1;i<=Q;i++)
	{
		scanf("%d",&e[i].opt);
		if(e[i].opt==1)
		{
			scanf("%d%d%d%d",&e[i].x0,&e[i].y0,&e[i].x2,&e[i].y2);
			slope[++top]=getslope(e[i].x0,e[i].y0);
			slope[++top]=getslope(e[i].x2,e[i].y0);
			slope[++top]=getslope(e[i].x0,e[i].y2);
		}
		if(e[i].opt==2)
		{
			scanf("%d%d",&e[i].x0,&e[i].y0);
			slope[++top]=getslope(e[i].x0,e[i].y0);
		}
	}
	sort(slope+1,slope+top+1);
	for(int i=top;i;i--)
	{
		if(!mp[slope[i]])cnt++;
		mp[slope[i]]=cnt;
	}
	build(1,1,cnt);
	for(int i=1;i<=Q;i++)
	{
		if(e[i].opt==1)
		{
			add(1,1,cnt,mp[getslope(e[i].x0,e[i].y0)],mp[getslope(e[i].x2,e[i].y0)],e[i].y0,i,0);
			add(1,1,cnt,mp[getslope(e[i].x0,e[i].y2)],mp[getslope(e[i].x0,e[i].y0)],e[i].x0,i,1);
		}
		else
		{
			ansx=ansy=make_pair(0x3f3f3f3f,0);
			ask(1,1,cnt,mp[getslope(e[i].x0,e[i].y0)]);
			if(!ansx.second||!ansy.second)printf("%d\n",ansx.second+ansy.second);
			else
			{
				if(!getslope(e[i].x0,e[i].y0))
				{
					if(e[ansx.second].x0<e[ansy.second].x0||ansx.second<ansy.second)printf("%d\n",ansx.second);
					else printf("%d\n",ansy.second);continue;
				}
				if(getslope(e[i].x0,e[i].y0)==0x3f3f3f3f)
				{
					if(e[ansx.second].y0<e[ansy.second].y0||ansx.second<ansy.second)printf("%d\n",ansx.second);
					else printf("%d\n",ansy.second);continue;
				}
				if(ansx.first==ansy.first*getslope(e[i].x0,e[i].y0))printf("%d\n",max(ansx.second,ansy.second));
				if(ansx.first<ansy.first*getslope(e[i].x0,e[i].y0))printf("%d\n",ansx.second);
				if(ansx.first>ansy.first*getslope(e[i].x0,e[i].y0))printf("%d\n",ansy.second);
			}
		}
	}
	return 0;
}

---

rp++