树状数组板子 x

树状数组!

参考 http://www.cnblogs.com/zzyh/p/6992148.html

洛谷 P3374 【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x k 含义：将第x个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出样例#1：

14
16

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

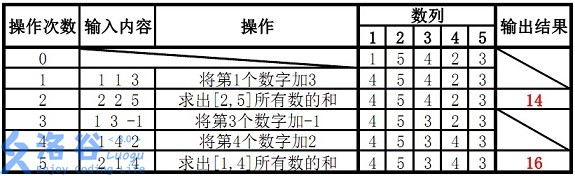
故输出结果14、16

思路:

　　单点增加,区间查询

上代码:

#include <iostream>
#include <cstdio>
#define lowbit(x) x&-x

using namespace std;

const int M = 5e5 + ;
int cc[M];
int n,m,a,b,c,x;

void add(int pos,int x)
{
    while(pos<=n)///更新后面的
    {
        cc[pos]+=x;
        pos+=lowbit(pos);
    }
}

int sum(int x,int y)
{
    x--;
///因为存储的是前缀和,然而x是点的坐标
///所以需要用右端点的前缀和减去[左端点减一]的前缀和
///所以直接x--
    int sum1=,sum2=;
    while(x)
    {
        sum1+=cc[x];
        x-=lowbit(x);
    }
    while(y)
    {
        sum2+=cc[y];
        y-=lowbit(y);
    }
    return sum2-sum1;///返回查询前缀和结果
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&x);
        add(i,x);
    }

    for(int i=;i<=m;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        if(a==)///单点增加
            add(b,c);
        else///区间查询
            printf("%d\n",sum(b,c));
    }
    return ;
}

洛谷 P3368 【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数数加上x

2.求出某一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含2或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x 含义：输出第x个数的值

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出样例#1：

6
10

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

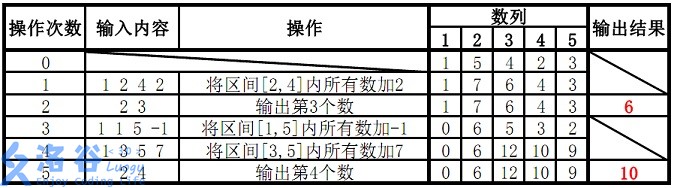
故输出结果为6、10

思路:

　　区间修改,单点查询

上代码:

#include <iostream>
#include <cstdio>
#define lowbit(x) x&-x

using namespace std;

const int M = 5e5 + ;
int cc[M];
int n,m,a,b,c,d,pre,x;

void add(int pos,int x)
{
    while(pos<=n)///更新后面的
    {
        cc[pos]+=x;
        pos+=lowbit(pos);
    }
}

int sum(int x)
{
    int sumd=;
    while(x)
    {
        sumd+=cc[x];
        x-=lowbit(x);
    }
    return sumd;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    {
        pre=x;
        scanf("%d",&x);
        add(i,x-pre);
    }

    for(int i=;i<=m;i++)
    {
        scanf("%d",&a);
        if(a==)///区间增加
        {
            scanf("%d%d%d",&b,&c,&d);
            add(b,d);
            add(c+,-d);
        }
        else///单点查询
            scanf("%d",&b),printf("%d\n",sum(b));
    }
    return ;
}

---

洛谷P2068 统计和

题目描述

给定一个长度为n（n<=100000），初始值都为0的序列，x(x<=10000)次的修改某些位置上的数字，每次加上一个数，然后提出y (y<=10000)个问题，求每段区间的和。时间限制1秒。

输入输出格式

输入格式：

第一行1个数，表示序列的长度n

第二行1个数，表示操作的次数w

后面依次是w行，分别表示加入和询问操作

其中，加入用x表示，询问用y表示

x的格式为"x a b" 表示在序列a的位置加上b

y的格式为"y a b" 表示询问a到b区间的加和

输出格式：

每行一个数，分别是每次询问的结果

输入输出样例

输入样例#1：

5
4
x 3 8
y 1 3
x 4 9
y 3 4

输出样例#1：

8
17

思路:

　　单点增加,区间查询

上代码:

#include <iostream>
#include <cstdio>
#define lb(x) (x&(-x))
using namespace std;

const int M = ;
int n,w;
int c[M];

void add(int pos,int x)
{
    while(pos<=n)
    {
        c[pos]+=x;
        pos+=lb(pos);
    }
}

int sum(int a,int b)
{
    a--;
    int sum1=,sum2=;
    while(a)
    {
        sum1+=c[a];
        a-=lb(a);
    }
    while(b)
    {
        sum2+=c[b];
        b-=lb(b);
    }
    return sum2-sum1;
}

int main()
{
    scanf("%d%d",&n,&w);
    char ch;
    for(int i=,a,b;i<=w;i++)
    {
        cin>>ch>>a>>b;
        if(ch=='x')
            add(a,b);
        else
            printf("%d\n",sum(a,b));
    }
    return ;
}

End.