leetcode-15双周赛-1289-下降路径最小和

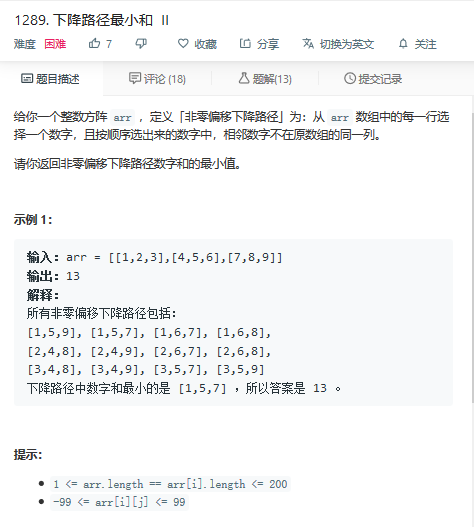
题目描述：

方法一：动态规划 O(N^3)

class Solution:
    def minFallingPathSum(self, arr: List[List[int]]) -> int:
        n = len(arr)
        for i in range(1,n):
            for j in range(n):
                arr[i][j] = arr[i][j] + min(arr[i-1][0:j] + arr[i-1][j+1:])
        return min(arr[-1])

优化：O(n^2logn)

class Solution:
    def minFallingPathSum(self, arr: List[List[int]]) -> int:
        n = len(arr)
        for i in range(1,n):
            a,b = sorted(arr[i-1])[::2]
            for j in range(n):
                arr[i][j] += a if arr[i - 1][j] != a else b
        return min(arr[-1])

优化：O(n^2)

class Solution:
    def minFallingPathSum(self, arr: List[List[int]]) -> int:
        n = len(arr)
        for i in range(1,n):
            a,b = float("inf"),float("inf")
            for j in arr[i-1]:
                if j < a:
                    if a != float("inf"):
                        b = a
                    a = j
                elif j < b:
                    b = j
            for j in range(n):
                arr[i][j] += a if arr[i - 1][j] != a else b
        return min(arr[-1])