UVa 10603 Fill (BFS && 经典模拟倒水 && 隐式图)

题意 ： 有装满水的6升的杯子、空的3升杯子和1升杯子，3个杯子中都没有刻度。不使用道具情况下，是否可量出4升水呢？

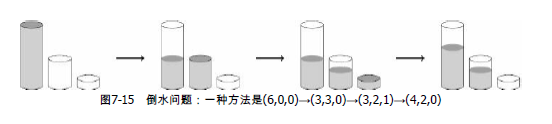
你的任务是解决一般性的问题：设3个杯子的容量分别为a, b, c，最初只有第3个杯子装满了c升水，其他两个杯子为空。最少需要倒多少升水才能让某一个杯子中的水有d升呢？如果无法做到恰好d升，就让某一个杯子里的水是d'升，其中d'<d并且尽量接近d。（1≤a,b,c,d≤200）。要求输出最少的倒水量和目标水量（d或者d'）。

分析 ： 紫书P202。

#include<bits/stdc++.h>
using namespace std;
 + ;
struct Node
{
    ], dist;
    bool operator < (const Node & rhs) const{//Caution!
        return dist > rhs.dist;
    }
};
];//learn->有近似解的存在，所以使用ans来保存d或者<d升水转移的水量，并
                     //且全部赋值-1，答案的查找和数组的初值有点类似背包刚好装满时候的处理
int vis[maxn][maxn];
inline void initialize()
{
    memset(ans, -, sizeof(ans));
    memset(vis, , sizeof(vis));
}
inline void update_ans(Node &temp)
{
    ; i<; i++){
        int Vol = temp.v[i];
         || ans[Vol] > temp.dist){//分别表示一开始和有更优解的情况
            ans[Vol] = temp.dist;
        }
    }
}
inline void solve(int a, int b, int c, int d)
{
    priority_queue<Node> pq;
    Node Fir_node;
    Fir_node.dist = ;
    Fir_node.v[] = , Fir_node.v[] = , Fir_node.v[] = c;
    pq.push(Fir_node);
    vis[][] = ;
    while(!pq.empty()){
        Node u = pq.top();
        pq.pop();
        update_ans(u);
        ) break;
        ; i<; i++){
            ; j<; j++){
                if(j!=i){
                     || u.v[j]==cap[j]) continue;//此过程描述i倒向j，所以在i空或j满的情况下是无法做到的。模拟的代码应多考虑实际意义。
                    int Trans = min(cap[j], u.v[i]+u.v[j]) - u.v[j];//注意这里是min
                    Node New;
                    memcpy(&New, &u, sizeof(u));//*learn->结构体也可以这样赋值
                    New.v[i] -= Trans;
                    New.v[j] += Trans;
                    New.dist = u.dist + Trans;
                    ]][New.v[]]){
                        pq.push(New);
                        vis[New.v[]][New.v[]] = ;
                    }
                }
            }
        }
    }
    ){
        ){
            printf("%d %d\n", ans[d], d);
            return ;
        }
        d--;
    }
}
int main(void)
{
    int nCase;
    scanf("%d", &nCase);
    while(nCase--){
        int a, b, c, d;
        initialize();
        scanf("%d %d %d %d", &a, &b, &c, &d);
        cap[] = a, cap[] = b, cap[] = c;
        solve(a, b, c, d);
    }
    ;
}

瞎 ：

①类似的倒水问题，模拟倒水的操作可以参考刘汝佳的代码，简洁

        ; i<; i++){
            ; j<; j++){
                if(j!=i){
                     || u.v[j]==cap[j]) continue;///此过程描述i倒向j，所以在i空或j满的情况下是无法做到的。
                    int Trans = min(cap[j], u.v[i]+u.v[j]) - u.v[j];//*max -> min
                    Node New;
                    memcpy(&New, &u, sizeof(u));//*->learn
                    New.v[i] -= Trans;
                    New.v[j] += Trans;
                    New.dist = u.dist + Trans;
                    ]][New.v[]]){
                        pq.push(New);
                        vis[New.v[]][New.v[]] = ;
                    }
                }
            }
        }

倒水

②对于此类初始和结束都知道的，考虑存储状态进行广搜操作，注意状态的定义

③如果对于每一次状态转移的某一权值有要求，可以考虑使用结构体存储状态入队，然后根据某一需要的元素进行重载小于号，队列则使用优先队列

④这道题的广搜解答树明显有许多末端节点，所以应该全都去与暂存的答案比较，而不是一搜到答案就OK，而类似最短路的模型则是一搜到就推出，因为权值就是路径，第一个搜到的肯定是路径最短的，而此题很明显并不是转化成了最短路模型，如果是求倒水次数最少的话则是，现在求的是倒水量，所以在考虑将一道题进行状态转化然后进行搜索的时候，要区别答案是如何找出来的。

⑤对于搜索而言，状态很重要，对于现在这个局面，哪几个关键的信息能表示现在的状态，如何判重，答案如何存储和状态如何转移，都是决定能不能或者如何搜索的关键。