[洛谷P2154] SDOI2009 虔诚的墓主人

问题描述

小W是一片新造公墓的管理人。公墓可以看成一块N×M的矩形，矩形的每个格点，要么种着一棵常青树，要么是一块还没有归属的墓地。

当地的居民都是非常虔诚的基督徒，他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚，他们希望自己的墓地拥有着较高的虔诚度。

一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地，墓地的正上、正下、正左、正右都有恰好k棵常青树。

小W希望知道他所管理的这片公墓中所有墓地的虔诚度总和是多少。

输入格式

输入文件religious.in的第一行包含两个用空格分隔的正整数N和M，表示公墓的宽和长，因此这个矩形公墓共有(N+1) ×(M+1)个格点，左下角的坐标为(0, 0)，右上角的坐标为(N, M)。

第二行包含一个正整数W，表示公墓中常青树的个数。

第三行起共W行，每行包含两个用空格分隔的非负整数xi和yi，表示一棵常青树的坐标。输入保证没有两棵常青树拥有相同的坐标。

最后一行包含一个正整数k，意义如题目所示。

输出格式

输出文件religious.out仅包含一个非负整数，表示这片公墓中所有墓地的虔诚度总和。为了方便起见，答案对2,147,483,648取模。

样例输入

5 6

13

0 2

0 3

1 2

1 3

2 0

2 1

2 4

2 5

2 6

3 2

3 3

4 3

5 2

2

样例输出

6

说明

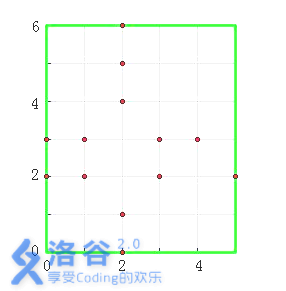
图中，以墓地(2, 2)和(2, 3)为中心的十字架各有3个，即它们的虔诚度均为3。其他墓

地的虔诚度为0。

对于30%的数据，满足1 ≤ N, M ≤ 1,000。

对于60%的数据，满足1 ≤ N, M ≤ 1,000,000。

对于100%的数据，满足1 ≤ N, M ≤ 1,000,000,000，0 ≤ xi ≤ N，0 ≤ yi ≤ M，1 ≤ W ≤ 100,000，1 ≤ k ≤ 10。

存在50%的数据，满足1 ≤ k ≤ 2。

存在25%的数据，满足1 ≤ W ≤ 10000。

解析

设点A上面有a棵树，下面有b棵树，左边有c棵树，右边有d棵树。那么，点A的虔诚度为

\[C_a^k*C_b^k*C_c^k*C_d^k
\]

在纵坐标相同的两棵树之间，所有墓地的左右数量不变，因此这些墓地的虔诚度之和就是左右的组合数的乘积再乘上每一列的组合数乘积之和。我们有如下做法：将每棵树按照纵坐标从小到大排序，纵坐标相同按横坐标从小到大排序。用树状数组维护每一列上的组合数乘积，即\(C_a^k+C_b^k\)。每次扫描一行，在两个相邻的树之间统计答案，用区间求和即可实现。每扫描一行后更新树状数组中的值。

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#define int long long
#define N 2000002
using namespace std;
const int mod=2147483648;
struct node{
	int x,y;
}a[N];
int n,m,w,t,i,j,k,vx[N],vy[N],c[N],sum[N],num[N],f[N][12],n1,n2;
int read()
{
	char c=getchar();
	int w=0;
	while(c<'0'||c>'9') c=getchar();
	while(c<='9'&&c>='0'){
		w=w*10+c-'0';
		c=getchar();
	}
	return w;
}
int my_comp(const node &a,const node &b)
{
	if(a.y==b.y) return a.x<b.x;
	return a.y<b.y;
}
int lowbit(int x)
{
	return x&(-x);
}
void add(int x,int y)
{
	for(int i=x;i<=n1;i+=lowbit(i)) c[i]=(c[i]+y+mod)%mod;
}
int ask(int x)
{
	int ans=0;
	for(int i=x;i>=1;i-=lowbit(i)) ans=(ans+c[i]+mod)%mod;
	return ans;
}
signed main()
{
	n=read();m=read();w=read();
	for(i=1;i<=w;i++){
		a[i].x=read(),a[i].y=read();
		vx[i]=a[i].x;
		vy[i]=a[i].y;
	}
	t=read();
	f[0][0]=1;
	for(i=1;i<=w;i++){
		f[i][0]=1;
		for(j=1;j<=t;j++) f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod;
	}
	sort(vx+1,vx+w+1);
	sort(vy+1,vy+w+1);
	sort(a+1,a+w+1,my_comp);
	n1=unique(vx+1,vx+w+1)-vx-1;
	n2=unique(vy+1,vy+w+1)-vy-1;
	for(i=1;i<=w;i++){
		a[i].x=lower_bound(vx+1,vx+n1+1,a[i].x)-vx;
		a[i].y=lower_bound(vy+1,vy+n2+1,a[i].y)-vy;
		sum[a[i].x]++;
	}
	i=j=1;
	int ans=0;
	while(i<=w){
		while(a[i].y==a[j].y) j++;
		int cnt=j-i,now=1;
		for(k=i+1;k<j;k++,now++){
			int l=a[k-1].x,r=a[k].x;
			ans=(ans+(ask(r-1)-ask(l)+mod)%mod*f[now][t]%mod*f[cnt-now][t]%mod)%mod;
		}
		for(k=i;k<j;k++){
			int p=a[k].x;
			add(p,-f[num[p]][t]*f[sum[p]-num[p]][t]%mod);
			num[p]++;
			add(p,f[num[p]][t]*f[sum[p]-num[p]][t]%mod);
		}
		i=j;
	}
	printf("%lld\n",(ans%mod+mod)%mod);
	return 0;
}