牛顿迭代法理论推导及python代码实现

公式不便于在这里编辑，所以在word中编辑好了，截图过来。

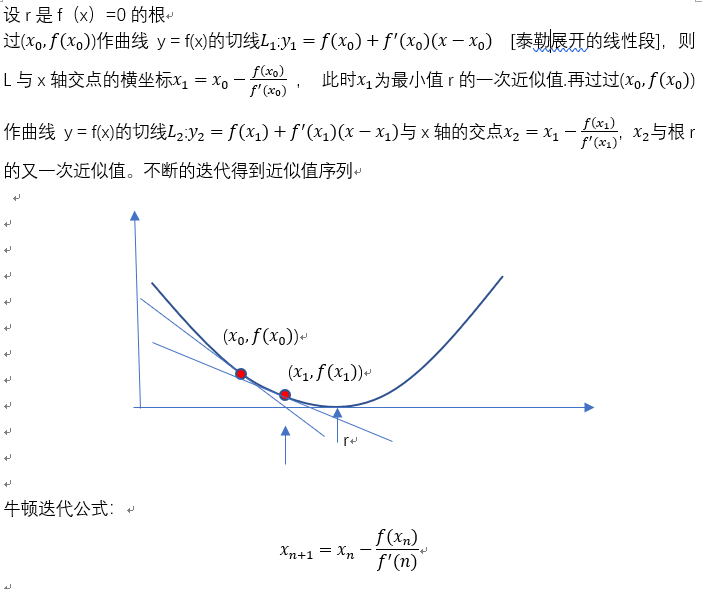
用python+牛顿迭代法   求 y =（x-2）**3的解

import numpy as np
import matplotlib.pyplot as plt
'''
牛顿迭代法实现 y =（x-2）**3的解
'''
def f(x):
    return (x-2)**3
def fd(x):
    return 3*((x-2)**2)
def newtonMethod(n,assum):
    time = n
    x = assum
    next = 0
    a = f(x)
    b = fd(x)
    print('a = '+str(a)+',b = '+str(b)+',time = '+str(time))
    if f(x) == 0.0:
        return time,x
    else:
        next = x-a/b
        print('next x = '+str(next))
    if a - f(next)<1e-6:
        print('meet f(x) = 0 , x = '+ str(next))  ##设置跳出条件，同时输出满足f(x) = 0 的x的值
    else:
        return newtonMethod(n+1,next)
 
newtonMethod(0,4.0)

C:\ProgramData\Anaconda3\python.exe D:/python/TensorFlow/算法实例/牛顿迭代法.py
a = 8.0,b = 12.0,time = 0
next x = 3.3333333333333335
a = 2.370370370370371,b = 5.333333333333334,time = 1
next x = 2.888888888888889
a = 0.7023319615912207,b = 2.3703703703703702,time = 2
next x = 2.5925925925925926
a = 0.20809835898999132,b = 1.0534979423868311,time = 3
next x = 2.3950617283950617
a = 0.0616587730340715,b = 0.4682213077274805,time = 4
next x = 2.263374485596708
a = 0.018269266084169365,b = 0.20809835898999157,time = 5
next x = 2.1755829903978054
a = 0.005413115876790937,b = 0.09248815955110752,time = 6
next x = 2.11705532693187
a = 0.001603886185715827,b = 0.04110584868938101,time = 7
next x = 2.078036884621247
a = 0.0004752255365083959,b = 0.01826926608416941,time = 8
next x = 2.052024589747498
a = 0.00014080756637285685,b = 0.008119673815186359,time = 9
next x = 2.034683059831665
a = 4.17207604067724e-05,b = 0.0036087439178606037,time = 10
next x = 2.023122039887777
a = 1.2361706787192059e-05,b = 0.0016038861857158443,time = 11
next x = 2.015414693258518
a = 3.662727936945795e-06,b = 0.0007128383047625975,time = 12
next x = 2.0102764621723455
a = 1.0852527220580603e-06,b = 0.00031681702433894134,time = 13
next x = 2.0068509747815635
meet f(x) = 0 , x = 2.0068509747815635
 
Process finished with exit code 0

从运行的结果可以看出近似根x = 2.0068509747815635