(js描述的)数据结构[树结构1.2](12）

1.先序遍历



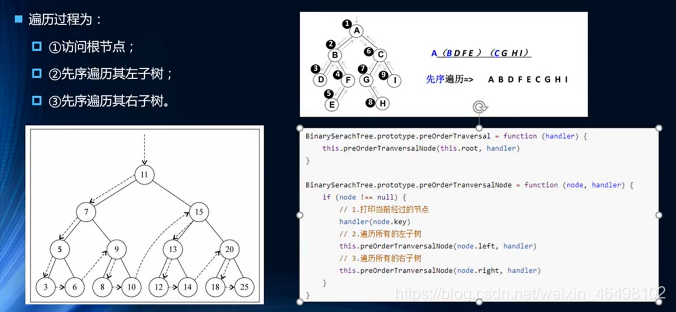
2.中序遍历



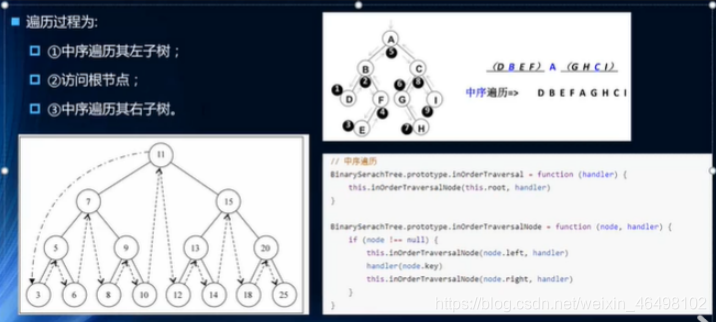
3.后序遍历



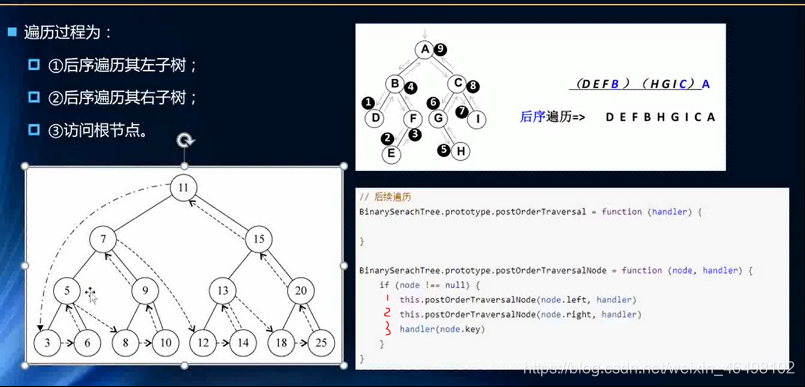
4.递归调用栈详解：



详细见： https://zhuanlan.zhihu.com/p/24291978

5.删除节点操作分析：



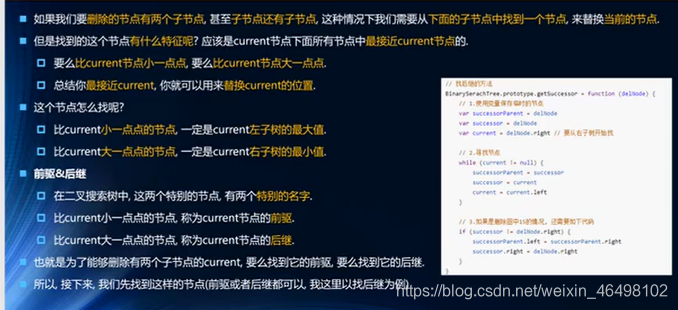
5.代码封装

 //封装二叉搜索树
        function BinarySearchTree() {
            //封装节点内部类
            function Node(key) {
                this.key = key
                this.left = null
                this.right = null
            }
            //属性
            this.root = null
            //方法
            // 1. insert方法
            BinarySearchTree.prototype.insert = function(key) {
                var newNode = new Node(key)
                if (this.root == null) {
                    this.root = newNode
                } else {
                    this.insertNode(this.root, newNode)
                }
            }
            //封装一个递归方法
            BinarySearchTree.prototype.insertNode = function(node, newNode) {
                if (newNode.key > node.key) {
                    if (node.left == null) {
                        node.left = newNode
                    } else {
                        this.insertNode(node.left, newNode)
                    }
                } else {
                    if (node.right == null) {
                        node.right = newNode
                    } else {
                        this.insertNode(node.right, newNode)
                    }
                }
            }

            // 遍历方式
            // 1. 先序遍历
            BinarySearchTree.prototype.preOrderTranversal = function(handle) { //handle 为传入的处理key的函数
                this.preOrderTranversalNode(this.ropot, handle)
            }
            //定义一个遍历节点的方法
            BinarySearchTree.prototype.preOrderTranversalNode = function(node, handle) {
                if (node !== null) {
                    handle(node.key)
                    // 先序遍历左节点
                    this.preOrderTranversalNode(node.left, handle)
                    //先序遍历右节点
                    this.preOrderTranversalNode(node.right, handle)
                }
            }
            // 2.中序遍历
            BinarySearchTree.prototype.midOrderTranversal = function(handle) { //handle 为传入的处理key的函数
                this.midOrderTranversalNode(this.ropot, handle)
            }
            //定义一个遍历节点的方法
            BinarySearchTree.prototype.midOrderTranversalNode = function(node, handle) {
                if (node !== null) {
                    // 先序遍历左节点
                    this.midOrderTranversalNode(node.left, handle)
                    handle(node.key)

                    //先序遍历右节点
                    this.midOrderTranversalNode(node.right, handle)
                }
            }
            // 3.后序遍历
            BinarySearchTree.prototype.postOrderTranversal = function(handle) { //handle 为传入的处理key的函数
                this.postOrderTranversalNode(this.ropot, handle)
            }
            //定义一个遍历节点的方法
            BinarySearchTree.prototype.postOrderTranversalNode = function(node, handle) {
                if (node !== null) {
                    // 先序遍历左节点
                    this.postOrderTranversalNode(node.left, handle)

                    //先序遍历右节点
                    this.postOrderTranversalNode(node.right, handle)
                    handle(node.key)

                }
            }
            // 寻找最值
            // 最大值
            BinarySearchTree.prototype.max = function() {
                var node = this.root
                while (node.right !== null) {
                    node = node.right
                }
                return node.key
            }
            // 最小值
            BinarySearchTree.prototype.min = function() {
                var node = this.root
                while (node.left !== null) {
                    node = node.left
                }
                return node.key
            }

            //搜索特定key

            BinarySearchTree.prototype.search  = function(key) {
                // 1.通过循环实现
                var node =this.root
                while (node !== null) {
                    if (node.key < key ) {
                        node = node.right
                    } else if(node.key > key) {
                        node = node.left
                    } else {
                        return true
                    }
                    return false
                }

                // 2.通过递归实现
                this.searchNode(this.root)
            }
            //递归函数封装
            BinarySearchTree.prototype.searchNode = function(node, key) {
                if (node == null) {
                    return false
                }
                if (node.key < key) {
                    this.searchNode(node.left)
                } else if(node.key > key) {
                    this.searchNode(node.right)
                } else {
                    return true
                }
            }
            //删除操作
            BinarySearchTree.prototype.remove = function(key) {
                var current = this.root
                var parent = null
                var isLeftChild = true
                //寻找key对应的节点
                while (current.key != key) {
                    parent = current
                    if (current.key < key) {
                        isLeftChild = true
                        current = current.right
                    } else {
                        isLeftChild = false
                        current = current.left
                    }
                    if (current == null) {
                        return false
                    }
                }
                //找到了key对应的节点
                // 删除的节点是叶子节点
                if(current.left == null && current.right == null) {
                    //是根节点
                    if(current == this.root) {this.root = null}
                    //
                    else { isLeftChild ? parent.left = null: parent.right =null}
                }
                //节点有一个子节点
                else if (current.left == null || current.right == null) {
                    //当前删除的节点是父节点的左节点
                    if (current == this.root) { this.root = current.left || current.right}
                    else if (isLeftChild) {
                        parent.left = current.left || current.right
                    }
                    //当前删除的节点是父节点的右节点
                    else{
                        parent.right = current.right || current.left
                    }
                }
                //节点有两个子节点
                else {
                    var successor = this.getSuccessor(current)
                    if (successor == this.root) {
                        this.root = successor
                    } else {
                        if (isLeftChild) {
                            parent.left = successor
                        } else {
                            parent.right = successor
                        }
                    }
                    successor.left = current.left
                }
            }
            //寻找后继的方法
            BinarySearchTree.prototype.getSuccessor = function(delNode) {
                var successor = delNode     //后继节点的父节点
                var current = delNode.right //后继节点的子节点
                var successorParent = delNode //后继节点
                while (current != null) {
                    successorParent = successor
                    successor = current
                    current = current.left
                }
                if (successor != delNode.right) { //当后继节点的不是删除节点的右节点时
                    successorParent.left = successor.right //把后记节点的右节点让后继节点的父节点的left指向它
                    successor.right = delNode.right //、把后继节点的右节点接上删除节点的右节点
                }
                return successor
            }
        }

删除操作总结: