2019-07-31【机器学习】无监督学习之降维NMF算法 （人脸特征提取）

代码

from numpy.random import RandomState #加载RandomState用于创建随机种子
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces
from sklearn import decomposition

n_row, n_col = 2, 3  #设置图像展示时的排列情况
n_components = n_row * n_col  #
image_shape = (64, 64) #设置人脸数据图片的大小

dataset = fetch_olivetti_faces(shuffle=True, random_state=RandomState(0)) #array 二维
#print(dataset)
faces = dataset.data #array 一维
#print(faces)

def plot_gallery(title, images, n_col=n_col, n_row=n_row):
    plt.figure(figsize=(2. * n_col, 2.26 * n_row)) #指定图片大小
    plt.suptitle(title, size=16) #设置标题和字号大小

    for i, comp in enumerate(images):
        plt.subplot(n_row, n_col, i + 1)#选择画制的子图
        vmax = max(comp.max(), -comp.min())

        plt.imshow(comp.reshape(image_shape), cmap=plt.cm.gray,
                   interpolation='nearest', vmin=-vmax, vmax=vmax)#对数值归一化，并以灰度图形显示
        plt.xticks(())
        plt.yticks(())#去除子图坐标轴标签
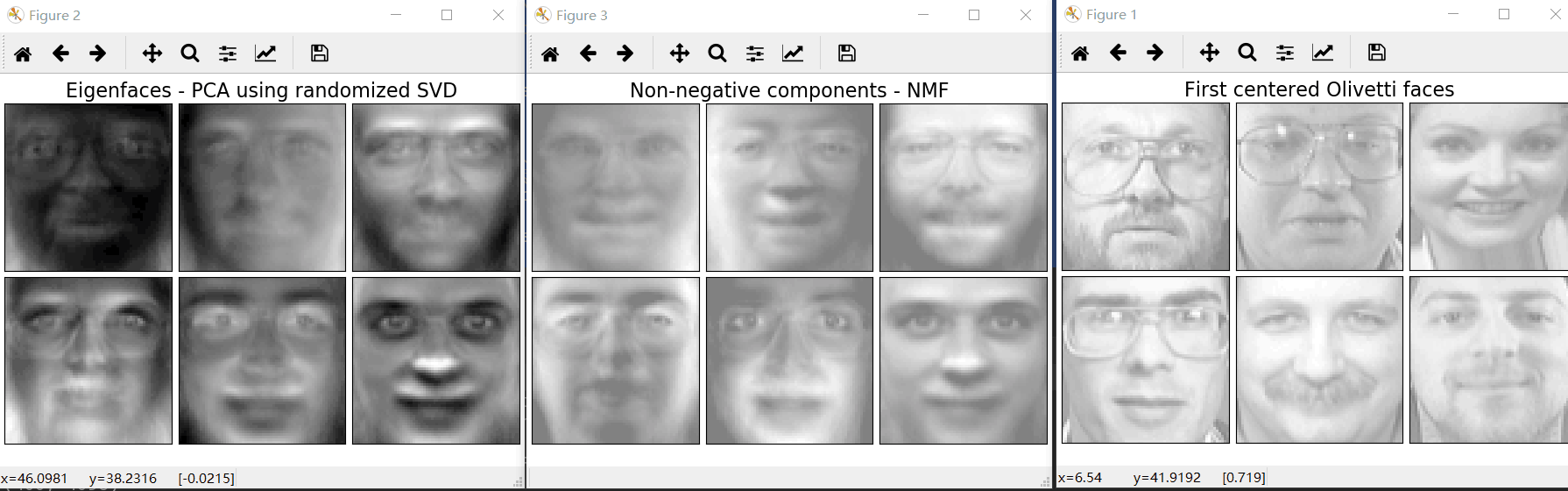
    plt.subplots_adjust(0.01, 0.05, 0.99, 0.93, 00.04, 0.) #设置子图位置和间隔调整

plot_gallery("First centered Olivetti faces", faces[:n_components])

estimators = [
    ('Eigenfaces - PCA using randomized SVD',
        decomposition.PCA(n_components=6, whiten=True)),
    ('Non-negative components - NMF',
        decomposition.NMF(n_components=6, init='nndsvda', tol=5e-3))
]

for name, estimator in estimators:
    #print(estimator)
    print("Extracting the top %d %s..."% (n_components, name))
    print(faces.shape) #输出图片大小 400，4096
    estimator.fit(faces) #调用算法提取特征
    components_ = estimator.components_ #获取提取的特征,一个二维列表
    #print(components_)
    plot_gallery(name, components_[:n_components]) #按照固定格式进行排列

plt.show()

效果图：