[图中找环] Codeforces 659E New Reform

New Reform

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Berland has n cities connected by m bidirectional roads. No road connects a city to itself, and each pair of cities is connected by no more than one road. It is not guaranteed that you can get from any city to any other one, using only the existing roads.

The President of Berland decided to make changes to the road system and instructed the Ministry of Transport to make this reform. Now, each road should be unidirectional (only lead from one city to another).

In order not to cause great resentment among residents, the reform needs to be conducted so that there can be as few separate cities as possible. A city is considered separate, if no road leads into it, while it is allowed to have roads leading from this city.

Help the Ministry of Transport to find the minimum possible number of separate cities after the reform.

Input

The first line of the input contains two positive integers, n and m — the number of the cities and the number of roads in Berland (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000).

Next m lines contain the descriptions of the roads: the i-th road is determined by two distinct integers xi, yi (1 ≤ xi, yi ≤ n, xi ≠ yi), where xi and yi are the numbers of the cities connected by the i-th road.

It is guaranteed that there is no more than one road between each pair of cities, but it is not guaranteed that from any city you can get to any other one, using only roads.

Output

Print a single integer — the minimum number of separated cities after the reform.

Examples

input

Copy

4 3
2 1
1 3
4 3

output

Copy

1

input

Copy

5 5
2 1
1 3
2 3
2 5
4 3

output

Copy

0

input

Copy

6 5
1 2
2 3
4 5
4 6
5 6

output

Copy

1

Note

In the first sample the following road orientation is allowed: , , .

The second sample: , , , , .

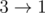The third sample: , , , , .

题意：有n个点m条边，一开始是双向边，现在要改为单边，问现在入度为0的点最少有多少个

思路：如果没环就必定会出现一个城市入度为0，所以就是如何找环，一种是dfs看是否有节点被重复访问，另一种是并查集看祖先是否是它本身且是否和其他环相连

 #include<bits/stdc++.h>
 using namespace std;
 const int amn=1e5+;
 vector<int> v[amn];
 bool idx[amn];
 int ans,f;
 void dfs(int x,int pre){
     if(idx[x]){f=;return;}
     idx[x]=;
     for(int i=;i<v[x].size();i++){
         int u=v[x][i];
         if(u==pre)continue;
         dfs(u,x);
     }
 }
 int main(){
     int n,m,u,t,len,le;
     ios::sync_with_stdio();
     cin>>n>>m;
     for(int i=;i<m;i++){
         cin>>u>>t;
         v[u].push_back(t);
         v[t].push_back(u);
     }
     for(int i=;i<=n;i++){
         if(!idx[i]){
             f=;
             dfs(i,);
             if(!f)ans++;
         }
     }
     printf("%d\n",ans);
 }

dfs找环

 #include<bits/stdc++.h>
 using namespace std;
 const int amn=1e5+;
 int pre[amn];
 bool idx[amn];
 int ans;
 int fd(int x){
     return x==pre[x]?x:pre[x]=fd(pre[x]);
 }
 int main(){
     int n,m,u,v,len,le;
     ios::sync_with_stdio();
     cin>>n>>m;
     for(int i=;i<=n;i++)pre[i]=i;
     for(int i=;i<m;i++){
         cin>>u>>v;
         int fu=fd(u),fv=fd(v);
         if(fu!=fv){
             pre[fu]=fv;
             if(idx[fu]||idx[fv]||idx[u]||idx[v])idx[fu]=idx[fv]=idx[u]=idx[v]=;
         }
         else idx[fu]=idx[fv]=idx[u]=idx[v]=;
     }
     for(int i=;i<=n;i++)if(fd(i)==i&&!idx[i])ans++;
     printf("%d\n",ans);
 }

并查集找环