Day1T1仓鼠的石子游戏——博弈论

打比赛的时候还没学博弈论，打完下来花了半个多小时学完，发现这题就是一道\(SG\)函数

其实当时差一点就\(YY\)出了答案，但是后面太难想，所以没整出来

机房大佬们都说自己没学博弈论，但是都AC

题解

假设先手兔子（我）放的是黑棋，仓鼠（小埋）放的是白棋

首先这道题的\(n\)个环可以认为是\(n\)个独立的\(G_1,G_2,G_3...\)有向图游戏，共同构成\(G\)游戏

那么$SG(G) = SG(G_1) $ \(XOR\) \(SG(G_2)\) \(XOR\) \(SG(G_3)......\)

所以我们只需要构造每个环的\(SG\)函数即可（本题其实不需要构造

咋构造啊

手玩一下样例，发现当\(a[i] = 1\)时有先手必胜态

其他的咋搞呢

好多人手玩样例赌了一下有先手必败态，然后还真的\(A\)了，就连题解都是这么写的……

然而正直的我没……

咳咳，首先有必败态当且仅当所有的空位置都在黑棋旁边。

那么我们就可以列出所有的必败态

首先空位置一定不能挨在一起，不然就可以填上某个颜色的棋

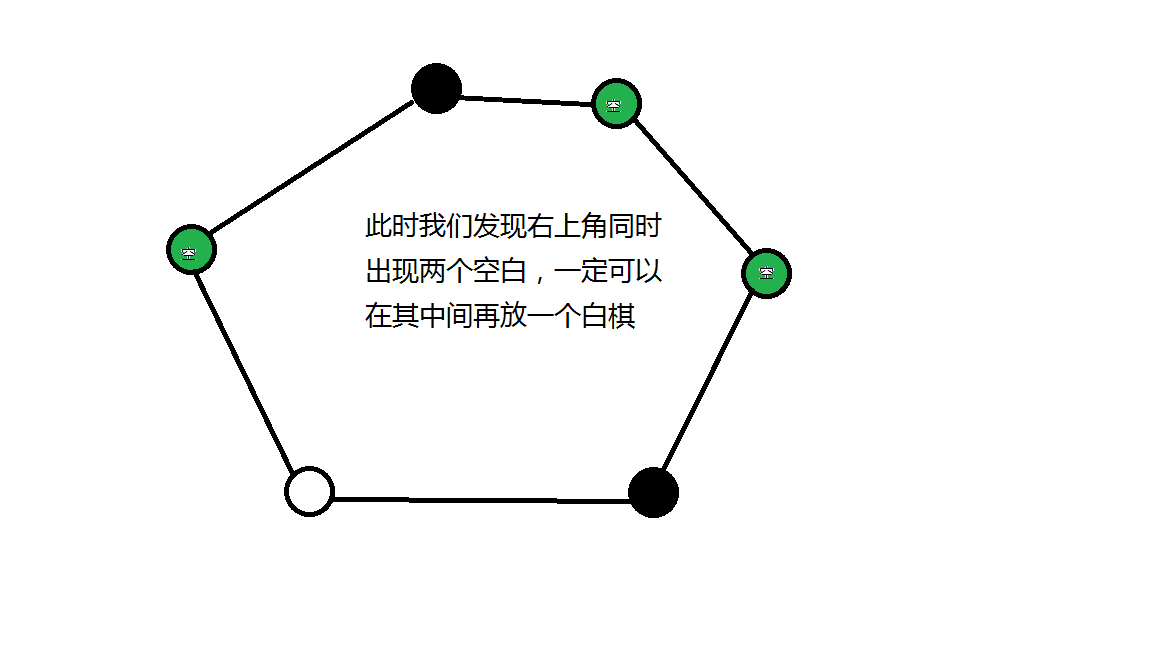
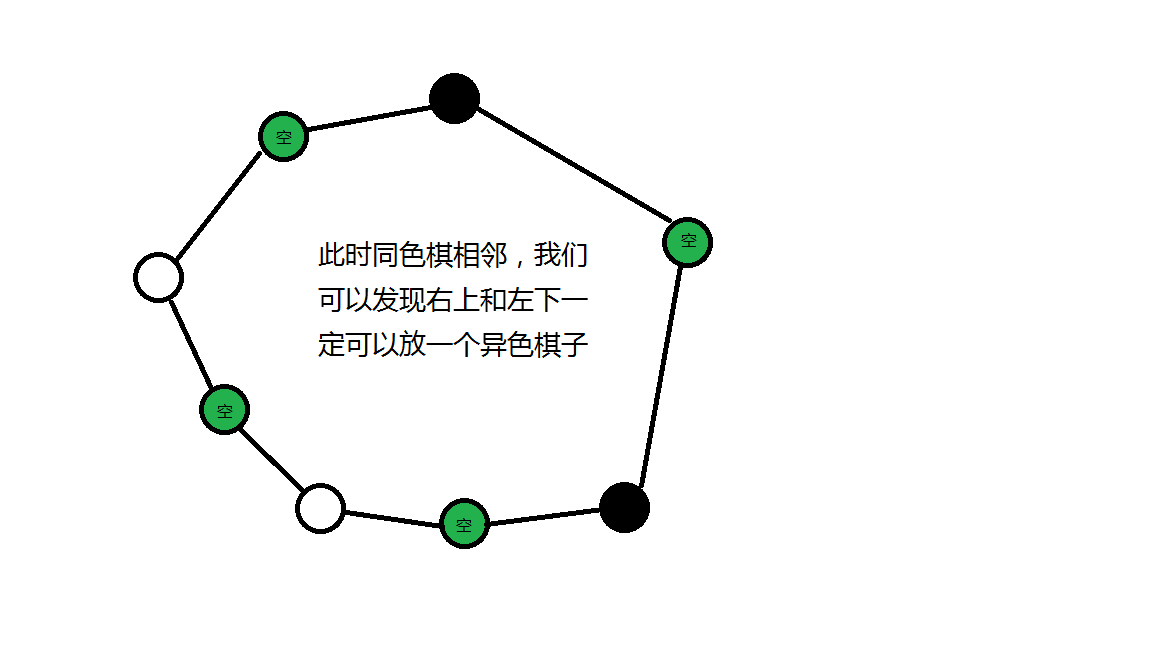
其次省略空位后黑棋白棋一定交替轮流出现，因为假如有两个相同颜色的棋相邻的话，其间必有一个空位，而这个空位可以填另一种颜色的棋

那么最后就可以说明最后黑棋白棋数量一定一样多

考虑奇偶性

当\(a[i]\)为奇数时，下一个轮到黑棋，黑棋如果要摆放，必须与另一个黑棋相邻，先手必败

当\(a[i]\)为偶数时，下一个轮到黑棋，黑棋没得走，先手必败

所以当$a[i] $不为\(1\)时，\(SG(G_i)\)均为\(0\)

为\(1\)时均为\(1\)

那么最后用\(SG\)函数\(XOR\)一下就可以了

代码：

#include<bits/stdc++.h>
using namespace std;
#define rint register int
#define s1 "rabbit\n"
#define s2 "hamster\n"
int n, a[1010], T;
int main( void ){
	scanf( "%d", &T );
	while( T-- ){
		memset( a, 0, sizeof( a ) );
		scanf( "%d", &n );
		for( rint i = 1; i <= n; i++ ){
			int temp; scanf( "%d", &temp );
			if( temp == 1 ) a[i] = 1;
			else a[i] = 0;
		}
		for( rint i = 2; i <= n; i++ ) a[1] ^= a[i];
		if( a[1] == 1 ) printf( s1 ); else printf( s2 );
	}
	return 0;
}