PageRank算法实现

基本原理

在互联网上，如果一个网页被很多其他网页所链接，说明它受到普遍的承认和信赖，那么它的排名就高。这就是PageRank的核心思想。

引用来自《数学之美》的简单例子：

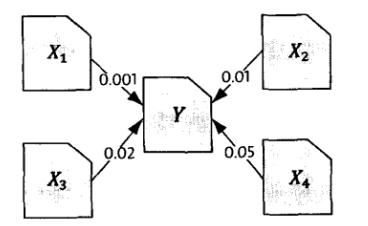
网页Y的排名应该来自于所有指向这个网页的其他网页的权重之和，在上图中Y的网页排名就是0.001 + 0.01 + 0.02 + 0.05 = 0.081。

如此，就可以把互联网简化成一个有向图，每个结点就代表一个网页，边就代表网页之间的链接关系。

接下来以具体的例子来介绍如何计算：

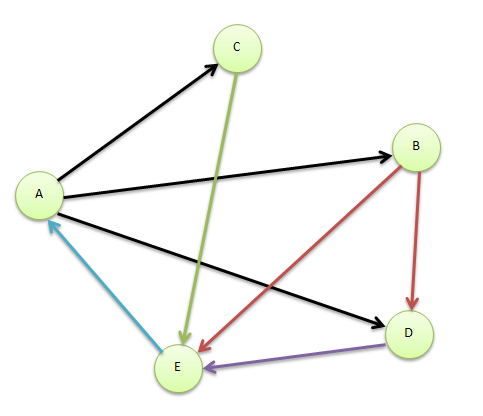
令 $PR = \left (PR_{1}\ ,\ PR_{2} \ ,\cdots ,PR_{N}\right )^{T}$为各个网页的排名，上图的网络用邻接矩阵来表示就是：

$S = \begin{pmatrix}
0 & 0& 0& 0& 1\\
1/3 & 0& 0& 0 &0 \\
1/3 & 0& 0& 0& 0\\
1/3 & 1/2& 0& 0 &0 \\
0& 1/2& 1& 1& 0
\end{pmatrix}$

注意，每一列的元素和为1。

需要额外注意的是，该算法要实现的前提之一是图必须是强连通的，所以如果网络中存在没有出链的结点，那么就需要处理一下。处理方法是让该结点对所有其他结点都有出链（包括它自身）。

PageRank算法是通过迭代来实现的，假定$PR_{i}$是第$i$次迭代的结果，那么

$PR_{i} = S\cdot PR_{i-1}$

当经过多次迭代后，最后得到一个稳定的PR值。

现在因为我们一开始不知道网页的初始排名，所以令$PR_{i} = \left (\frac{1}{N}\ ,\ \frac{1}{N} \ ,\cdots ,\frac{1}{N}\right )^{T}$。

上文说到图必须是强连通的，除了存在没有出链的结点，还存在只对自己出链的结点，若是访问了此结点，那就一直在该结点处循环。当然了，我们可不会一直很傻的在该网页停留，在现实中，我们也会通过输入一个新的地址来访问别的网页，这个网页是随机的，和当前网页可以没有关系。

为此引入一个新的变量$\alpha $，表示用户以$\alpha $的概率访问该网页所链接的网页，以$1-\alpha $的概率随机访问图中任意网页。

新的迭代公式就是：

$PR_{i} = \frac{1-\alpha }{N}\cdot e^{T}\cdot e + \alpha *S\cdot PR_{i-1} $

其中$e^{T}$为全1的列向量。

Python算法实现

接下来就用python来计算上面的网页排名，代码如下：

 import numpy as np

 def page_rank(graph, alpha, eps, max_step):
     node = graph.shape[0]  # 网络中结点个数

     pr = []
     for i in range(node):  # 初始访问概率
         pr.append(1/node)

     pr = np.array(pr)
     pr = pr.reshape(pr.shape[0], 1)

     y = []                 # 跳转至任意网页的概率
     x = (1.0-alpha)/node
     for i in range(node):
         y.append(x)
     y = np.array(y)
     y = y.reshape(y.shape[0], 1)

     for i in range(max_step):
         pre_pr = pr
         pr = np.dot(alpha * graph, pr) + y

         if abs(np.min(pr - pre_pr)) < eps:
             print("The algorithm converges to the %dth iteration!" % i)
             print(pr)
             return

     print("failed!")

 if __name__ == '__main__':
     graph = np.array([[0, 0, 0, 0, 1],
                       [1/3, 0, 0, 0, 0],
                       [1/3, 0, 0, 0, 0],
                       [1/3, 1/2, 0, 0, 0],
                       [0, 1/2, 1, 1, 0]])
     page_rank(graph, 0.85, 1e-6, 100)

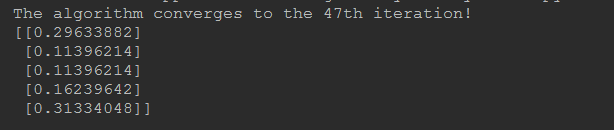
最后的运行结果：

MapReduce实现

这部分我也是用Python代码实现的，想看的可以转至我的另一篇随笔：传送文

参考：

[1] 【机器学习】【PageRank算法-1】PageRank算法原理介绍

[2] PageRank算法--从原理到实现

[3] 吴军. 数学之美. PageRank——Google的民主表决式网页排名技术