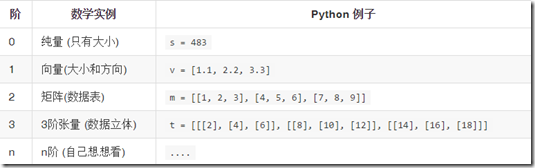
Tensorflow描述张量的维度：阶，形状以及维数

张量

TensorFlow用张量这种数据结构来表示所有的数据.你可以把一个张量想象成一个n维的数组或列表.一个张量有一个静态类型和动态类型的维数.张量可以在图中的节点之间流通。

阶

在TensorFlow系统中，张量的维数来被描述为阶。但是张量的阶和矩阵的阶并不是同一个概念。张量的阶（有时是关于如顺序或度数或者是n维）是张量维数的一个数量描述。

比如，下面的张量（使用Python中list定义的）就是2阶。

 t = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

你可以认为一个二阶张量就是我们平常所说的矩阵，一阶张量可以认为是一个向量。对于一个二阶张量你可以用语句t[i, j]来访问其中的任何元素。而对于三阶张量你可以用't[i, j, k]'来访问其中的任何元素。

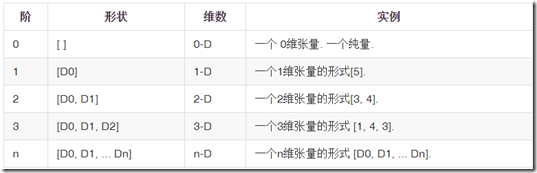
TensorFlow文档中使用了三种记号来方便地描述张量的维度：阶，形状以及维数.下表展示了他们之间的关系：

数据类型

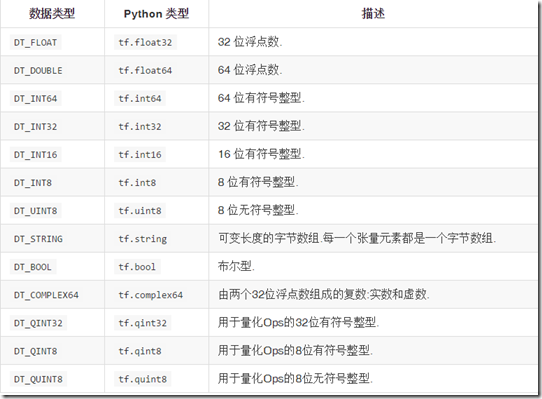
除了维度，Tensors有一个数据类型属性.你可以为一个张量指定下列数据类型中的任意一个类型：