主席树 【权值线段树】 && 例题K-th Number POJ - 2104

一、主席树与权值线段树区别

主席树是由许多权值线段树构成，单独的权值线段树只能解决寻找整个区间第k大/小值问题（什么叫整个区间，比如你对区间[1,8]建立一颗对应权值线段树，那么你不能询问区间[2,5]第k大/小值，你只能询问[1,8]第k大/小值问题）

二、权值线段树是什么鬼

学权值线段树之前你肯定要知道线段树，线段树是对区间中的所有数进行维护

权值线段树维护的对象和它不同，权值<==>这个数在这个区间中出现的次数

例如1、5、3、2、4

建立的权值线段树：

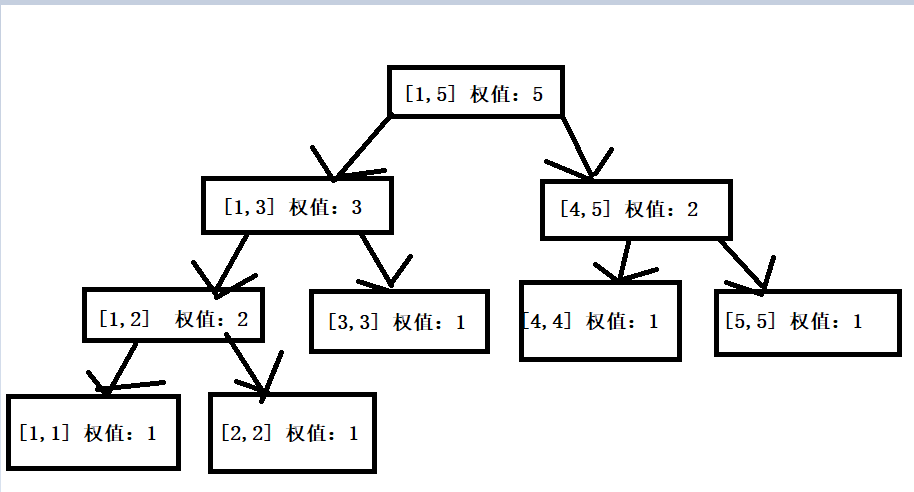
你会发现，权值线段树的建立和线段树不一样，线段树要考虑每一个数在区间中的位置

但是权值线段树不用管，相当于排完序之后建立的一颗树  。   要注意：权值代表这个数出现了几次

例如：我们寻找这个区间的第3小值

我们从根节点[1,5]的左节点来判断，因为左节点的权值要大于3，所以区间内第3小值肯定在根节点的左区间内

我们再看区间[1,3]的左节点，发现它的左节点权值为2小于3，所以答案肯定在区间[1,3]的右节点内。注意：这个时候我们要在右节点内寻找第3-2小值

之后那区间[3,3]内第1小值肯定就是3本身了

要注意如果题目给你的数据特别大，例如1、1000、200000000这三个数，我们要是直接建立权值线段树，那内存就炸了

所以这个时候就要离散化处理

三、主席树构成

我们文章开头说过，主席树是由许多权值线段树构成，而且主席树可以解决：在对应区间建立的主席树，可以找寻该区间所有子区间内的第k大/小值

（即、对区间[1,5]建立主席树，那么我们也可以找寻区间[1,3]的第k大/小值）

1、解决方法1：

排序后找到那个位置输出（不用想了，暴力方法肯定会被卡）

2、解决方法2：

对于一个区间[l, r]我们用一个用这个区间内出现过的数的个数组成一颗权值线段树，然后查询就完事了

但是多次询问区间第k小，我们每次这样建立一个线段树，这样不仅空间复杂度非常之高，而且时间复杂度也非常高，甚至比普通排序还要高，那么我们只不是可以想一个办法，使得对于每次我们查询不同的区间我们不需要重新建树，如果这样。时间复杂度和空间复杂度就大大降低了。

3、解决方法3：

这就用到了前缀和，比如我们有一个问题。就是每次静态的求区间和，我们可以预处理所以的前缀和sum[i]，我们每次求解区间[l, r]和时，我们可以直接得到答案为sum[r] - sum[l -1],这样就不需要对区间中的每个数进行相加来求解了。（这里我们设sum[i]中放的是权值线段树上i节点的权值）

想到就写起来

我们可以对区间[1,5]建立6棵权值线段树，分别是[0,0],[1,1],[1,2],[1,3],[1,4],[1,5] （[0,0]是一颗空树）

这样我们处理任意区间[l, r]时就可以通过处理区间[1,l - 1], [1,r]，就行，然后两者的处理结果进行相加相减就行。为什么满足相加减的性质，我们简单分析一下就很容易得出。如果在区间[1,l - 1]中有x个数小于一个数，在[1,r]中有y个数小于那个数，那么在区间[l,r]中就有y - x 个数小于那个数了，这样就很好理解为什么可以相加减了，另外，每颗树的结构都一样，都是一颗叶节点为n个的线段树。

上述利用前缀和的思想只是解决了时间复杂度的问题，并没有解决空间复杂度的问题，要解决空间复杂度问题。我们需要用到线段树的性质，我们每次更新一个数，那么与更新之前相比，这颗线段树改变只是一条链（从根节点到某一叶节点），那么我们可以充分利用这个特点，因为第i颗树与第i- 1颗树相比，只是更新了第i个元素，那么实际上第i颗树与第i-1颗树之间只有log个节点的信息是不同的。.所以这两棵树有很多相同的节点，所以这两棵树可以共用很多节点，也就是说，我们在第i-1颗树上 插入一个节点a[i] 得到第i颗权值线段树，而单点插入过程中只会修改根到那个叶子节点的路径上的那log个节点。于是这样就解决空间复杂度问题。

还是以上面的1、3、2、5、4为例子：

1、刚开始的空树

2、加一个1节点

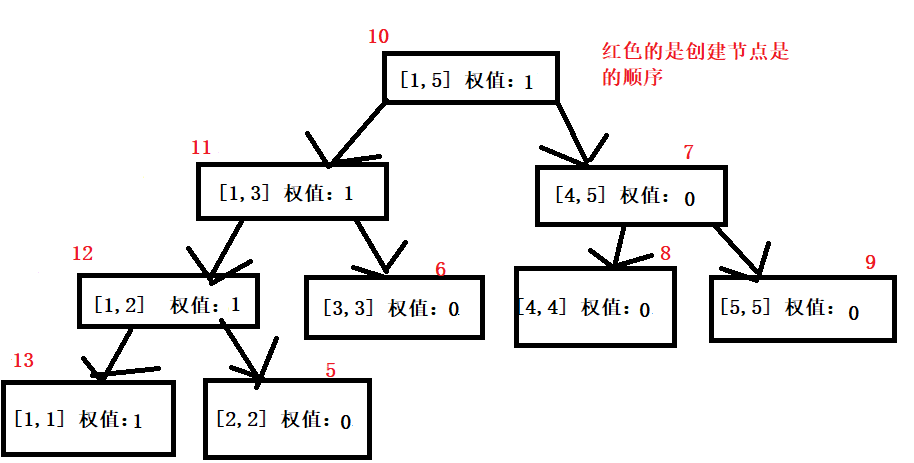
3、加一个2节点

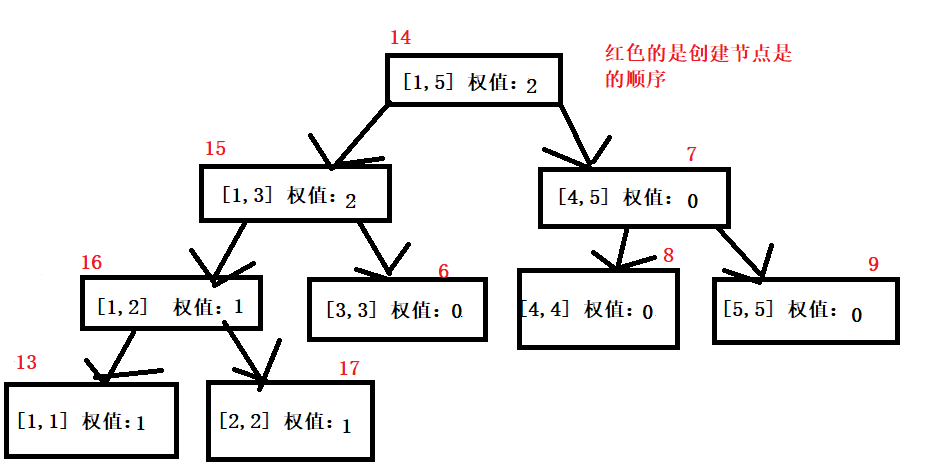
4、加一个节点3

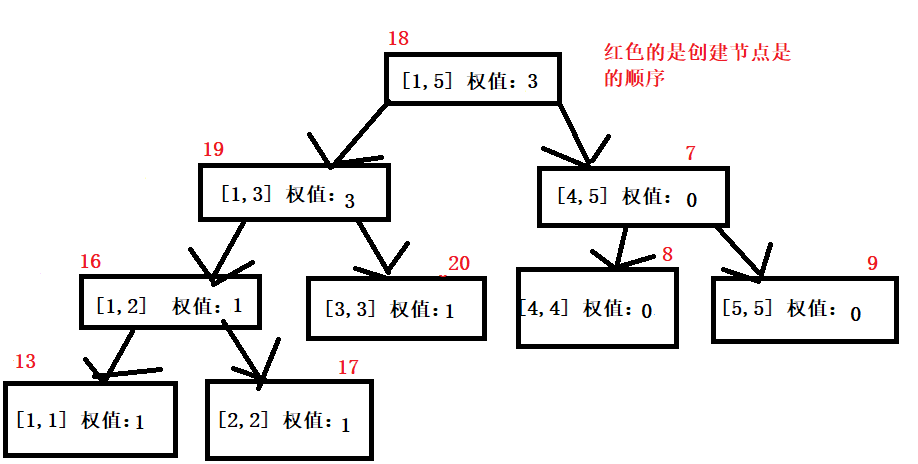
后面的4和5号节点就不写了，大家懂了就行。。。

四、主席树复杂度

插入一个点的时空复杂度都为O(log n),所以建立这颗主席树【权值线段树总体】的时空复杂度就是O(n log n),单次询问经过log n个节点，时间复杂度也为O(log n)

5、例题

K-th Number  POJ - 2104

代码1：

 1 #include<stdio.h>
 2 #include<iostream>
 3 #include<algorithm>
 4 #include<string.h>
 5 using namespace std;
 6 const int maxn=1e5+10;
 7 int cnt,ranks[maxn],v[maxn],root[maxn];
 8 struct shudui
 9 {
10     int value,id;
11 }w[maxn];
12 struct Node
13 {
14     int l,r,sum;
15     Node(){
16         sum=0;
17     }
18 }tree[maxn*20];
19 bool mmp(shudui x,shudui y)
20 {
21     return x.value<y.value;
22 }
23 void init()
24 {
25     cnt=1;
26     root[0]=0;
27     tree[0].l=tree[0].r=tree[0].sum=0;
28 }
29 void inserts(int num,int &rt,int l,int r)
30 {
31     tree[cnt++]=tree[rt];
32     rt=cnt-1;
33     tree[rt].sum++;
34     if(l==r) return;
35     int mid=(l+r)>>1;
36     if(num<=mid) inserts(num,tree[rt].l,l,mid);
37     else inserts(num,tree[rt].r,mid+1,r);
38 }
39 int query(int i,int j,int k,int l,int r)
40 {
41     int d=tree[tree[j].l].sum-tree[tree[i].l].sum;
42     if(l==r) return l;
43     int mid=(l+r)>>1;
44     if(k <= d) return query(tree[i].l, tree[j].l, k, l, mid);  //这里是小写的L,mid可不是数字1
45     else return query(tree[i].r, tree[j].r, k - d, mid + 1, r);
46 }
47 int main()
48 {
49     int n,m;
50     scanf("%d%d",&n,&m);
51     for(int i=1;i<=n;++i)
52     {
53         scanf("%d",&w[i].value);
54         w[i].id=i;
55     }
56     sort(w+1,w+1+n,mmp);
57     w[0].value=-1;
58     int j=1;
59     for(int i=1;i<=n;++i)
60     {
61         if(w[i].value!=w[i-1].value)
62             ranks[w[i].id]=j,v[j]=w[i].value,j++;
63         else ranks[w[i].id]=j-1;
64     }
65     init();
66     for(int i=1;i<=n;++i)
67     {
68         //printf("%d %d\n",ranks[i],v[i]);
69         root[i]=root[i-1];
70         inserts(ranks[i],root[i],1,n);
71     }
72     while(m--)
73     {
74         int l,r,x;
75         scanf("%d%d%d",&l,&r,&x);
76         printf("%d\n",v[query(root[l-1],root[r],x,1,n)]);
77     }
78     return 0;
79 }

代码2：

  1 //洛谷 P3834 可持久化线段树（主席树）
  2
  3 #include<cstdio>
  4
  5 #include<cstring>
  6
  7 #include<algorithm>
  8
  9 using namespace std;
 10
 11 const int N=200005;
 12
 13 int n,m,q,t=0;
 14
 15 int a[N],b[N],root[N];
 16
 17 struct node
 18
 19 {
 20
 21     int ls,rs,sum;
 22
 23 }tree[N*20];
 24
 25 void disc()
 26
 27 {
 28
 29     int i;
 30
 31     sort(b+1,b+n+1);
 32
 33     m=unique(b+1,b+n+1)-(b+1);
 34
 35     for(i=1;i<=n;++i)
 36
 37       a[i]=lower_bound(b+1,b+m+1,a[i])-b;
 38
 39 }
 40
 41
 42
 43 //insert函数就是说：当前插入的数p，会影响节点x，所以把x节点的sum加1.
 44
 45
 46
 47 //节点x代表一个权值区间，影响x就是说p在节点x所代表的权值区间内。
 48
 49 //那么先把前一个树的对应区间的节点复制过来，再加1，就行了。
 50
 51 //可以结合刚才的图感性理解一下。
 52
 53 void insert(int y,int &x,int l,int r,int p)
 54
 55 {
 56
 57     x=++t;    //t相当于是一个节点的地址，每个节点是不同的。
 58
 59     tree[x]=tree[y];    //复制前一个树的对应节点【它们代表的权值区间相同】。
 60
 61     tree[x].sum++;      //给这个节点的sum加1.（这个1指的就是p）
 62
 63     if(l==r)  return;   //搜索到根节点就返回。
 64
 65     int mid=(l+r)>>1;
 66
 67
 68
 69     //判断在哪个区间继续插入。
 70
 71     if(p<=mid)  insert(tree[y].ls,tree[x].ls,l,mid,p);
 72
 73     else  insert(tree[y].rs,tree[x].rs,mid+1,r,p);
 74
 75 }
 76
 77
 78
 79 //k是查询第k小
 80
 81 //x和y相当于是树的节点的地址。而l和r就是这两个节点的权值区间。
 82
 83 //一开始query(root[l-1],root[r],1,m,k)。
 84
 85 //root[l-1]就是第l-1颗树的根节点。root[r]就是第r颗树的根节点。
 86
 87 //比较它们左儿子代表的区间中的数的个数，差值为delta。根据delta判断这两个节点一起往哪个方向跳。
 88
 89 //分析过程和刚才二分的过程一样。
 90
 91 int query(int x,int y,int l,int r,int k)
 92
 93 {
 94
 95     if(l==r)  return l;    //查到权值线段树的叶子节点就返回这个值。
 96
 97     int delta=tree[tree[y].ls].sum-tree[tree[x].ls].sum;
 98
 99     int mid=(l+r)>>1;
100
101     if(k<=delta)  return query(tree[x].ls,tree[y].ls,l,mid,k);
102
103     else  return query(tree[x].rs,tree[y].rs,mid+1,r,k-delta);
104
105 }
106
107 int main()
108
109 {
110
111     int l,r,i,k;
112
113     scanf("%d%d",&n,&q);
114
115     for(i=1;i<=n;++i)
116
117     {
118
119         scanf("%d",&a[i]);
120
121         b[i]=a[i];
122
123     }
124
125     disc();
126
127     for(i=1;i<=n;++i)
128
129       insert(root[i-1],root[i],1,m,a[i]);
130
131     for(i=1;i<=q;++i)
132
133     {
134
135         scanf("%d%d%d",&l,&r,&k);
136
137
138
139         //query函数返回的是第k小的权值。
140
141         //把这个权值转化为原来这个权值对应的数就行了。
142
143         printf("%d\n",b[query(root[l-1],root[r],1,m,k)]);
144
145     }
146
147     return 0;
148
149 }

参考博客：

https://blog.csdn.net/g21glf/article/details/82986968

https://blog.csdn.net/creatorx/article/details/75446472