3. Linear Regression with Multiple Variables

前面还有一章主要讲解，基本的Linear Algebra线性代数的知识，都比较简单，这里就直接跳过了。

Speaker: Andrew Ng

---

1. Multiple featues

训练集的特征变成了多个，就是有多个的输入变量，对应一个的输出变量，但仍然是线性的关系。

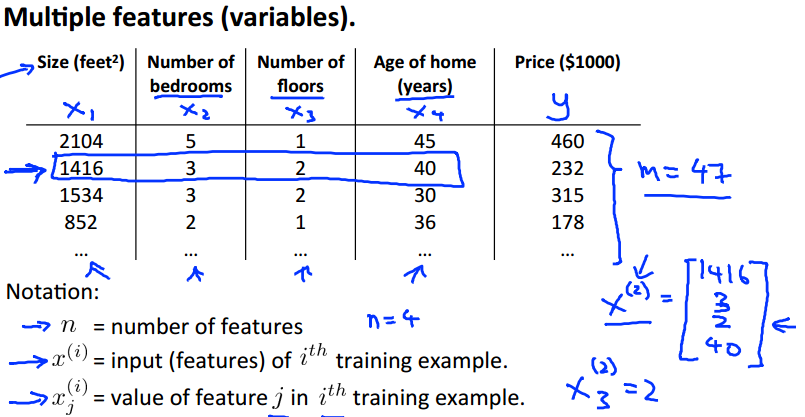
其中columns为 n 类特征，rows为 m 个samples，代表 i 个sample数据，代表第 i 个sample数据的第 j 个特征的值。

接下来我们定义在多变量下的：

其中针对通常的情况认为为1，这里通过向量表示为：

      

那么   

---

2. Gradient descent for multiple variable

下面来看一下多变量下梯度下降算法的定义：

Hypothesis : 

Parameters :     共n+1个参数

Cost Function :  

Gadient Descent :

Repeat {

    simultaneously update for every 

}

原来单变量的梯度下降算法与现在对变量的梯度下降算法比较，最关键的就是一定要同时进行更新。

---

3. Gradient descent in practice I : Feature Scaling 

这部分主要讲解Feature Scaling特征尺度对于梯度下降算法的影响。

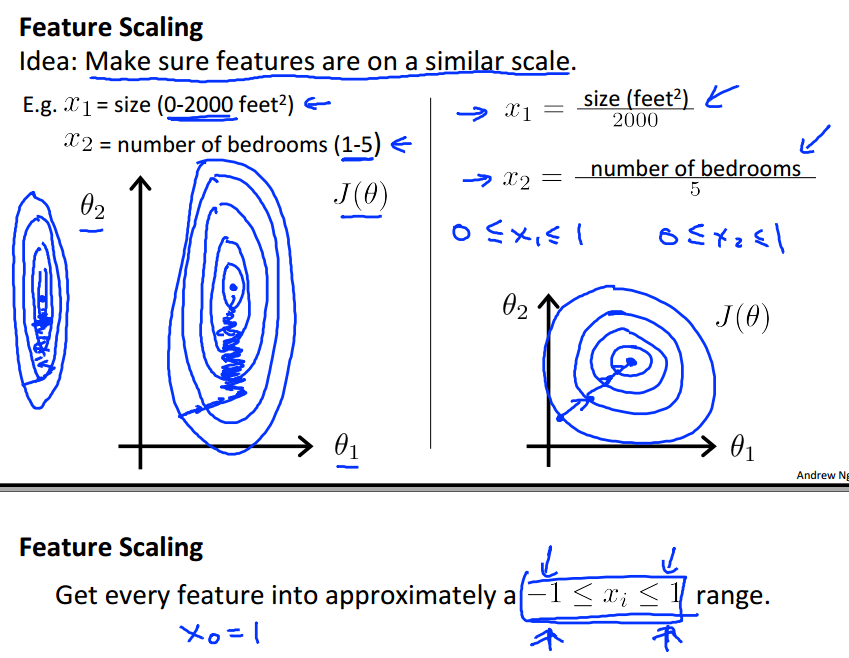
如果对于sample中的不同特征所处的范围差异很大，就像左图所示，那么使用梯度下降算法需要很长的时间才能找到局部最优解。

如果对于sample中的特征尺度进行数据标准化处理，例如把特征值处理到-1到1的范围内，那么梯度下降算法找寻局部最优解的时间就会大大减少。

在PPT中数据标准化的处理方法如下，，其中是range (max-min) , 或者是的标准差Standard  Deviation.

其他的数据标准化处理搜索可以找到很多，这里

---

4. Gadient descent in pratice II : Learing rate

梯度下降：

怎样保证梯度下降算法是正确在运行的，如何去选择一个合适的Learning Rate。

梯度下降算法收敛所需要的迭代次数是根据不同的模型而不同，通过绘制代价函数和迭代次数的关系图，或是把代价函数的变化值同阈值作比较，例如0.001，来判断收敛。

梯度下降算法还受到Learnin rate的影响，如果过小，收敛速度会非常慢，需要迭代很多次，如果过大，迭代可能使代价函数不收敛跳过局部最优值。

通常可以尝试以下的Learning rate: ..., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, ...

---

5. Features and polynomial regression

这里讲解多项式回归。对于线性回归可能并不能应用到所有数据，有些模型可能需要曲线来进行回归。比如Quadratic二次或Cubic三次模型。

例如: 以及下图所示

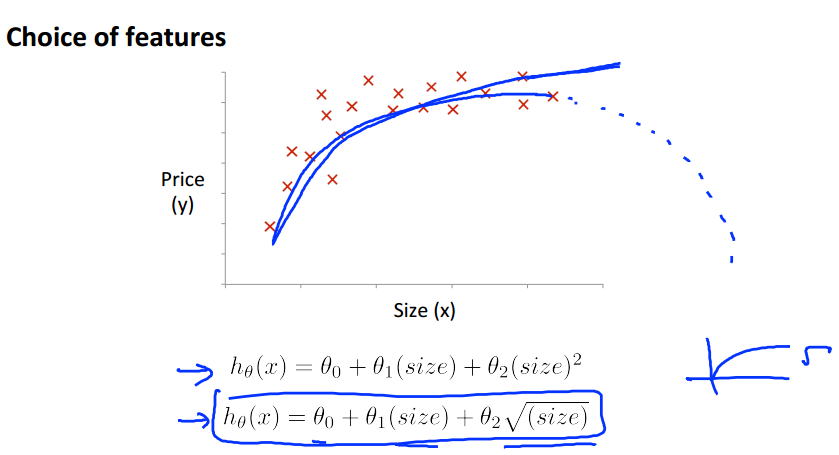
我们可以令，这样又变成了线性回归模型。当采用梯度下降时候，要记得进行特征尺度变换。

---

6. Normal equation

Normal equation是从线性代数的角度来求解方程，找到代价函数最小的参数，即求解

即希望，那么我们的训练矩阵为，训练集结果为，那么可以进行如下推导:

   (两边同乘以化为方阵)

     (两边同乘以)

即。

这里需要注意的是，可能是奇异矩阵、不可逆矩阵，一般使用Matlab或Octave时候使用pinv伪逆来进行计算。

如果遇到不可逆，我们可以考虑精简特征表示，或者特征太多(m <= n) ，而sample比较少，那么考虑删除特征，或者采用Regularization方式。

下面是对梯度下降算法和Normal equation的方法进行对比：

Gradient Descent	Normal Equation
需要选择合适的Learning rate	不需要设置参数
需要多次迭代Iteration	一次运算得到结果
可以适用于特征数量n很大的情况	如果特征数量n很大，运算时间代价就会很大， 因为矩阵逆的计算时间复杂度为O（n^3） 通常来说对于n小于10000可以考虑使用Normal Equation
适用于各种类型的模型	适用于线性模型，不适合逻辑回归模型或一些其他模型

参考：

http://files.cnblogs.com/gyj0715/courseramlnotes.pdf

http://www.cnblogs.com/elaron/archive/2013/05/20/3088894.html