[机器学习 ]PCA降维--两种实现 : SVD或EVD. 强力总结. 在鸢尾花数据集(iris)实做

PCA降维--两种实现 : SVD或EVD. 强力总结. 在鸢尾花数据集(iris)实做

今天自己实现PCA,从网上看文章的时候,发现有的文章没有搞清楚把SVD(奇异值分解)实现和EVD(特征值分解)实现,查阅多个文章很容易更糊涂,所以搞懂之后写下这个总结. 先说最关键的点:

a. PCA两个主要的实现方式: SVD(奇异值分解), EVD(特征值分解).

b. 特征值分解方式需要计算协方差矩阵,分解的是协方差矩阵.

 SVD方式不需要计算协方差矩阵,分解的是经过中心化的原数据矩阵

1.特征值分解实现PCA (也有人称为PCA原始算法)

然后把中心化过的矩阵 X 乘 W, 就得到了低维数据.

2.SCD分解实现PCA

(1)样本中心化得到矩阵X
(2)对X进行SVD分解 u s v = svd(X)
(3)取v的前dd个分量
(4)X*v[0:dd]就是低维空间的数据.
(这是对应X每一行为一个样本的情况.u用于行数的压缩,v用于列数的压缩)

3.Show Me the Code

import numpy as np
from numpy.linalg import svd
from numpy.linalg import eig
from sklearn import datasets    # 从sklearn中调出数据集
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

iris = datasets.load_iris()
data_src = iris.data    #(150,4)
labels = iris.target    #(150,)

d = 2       #设置低维空间维数

data_cen = data_src - np.mean(data_src,axis=0)  # 样本中心化处理

# 用 SVD(奇异值分解) 做PCA
def pca_svd():
    u, s, v = svd(data_cen)
    pc_svd = np.dot(data_cen, v[:,0:2])
    plt.scatter(pc_svd[:,0], pc_svd[:,1], c = labels)
    plt.show()
    return pc_svd

# 用 EVD(特征值分解) 做PCA
def pca_eig():
    cov_mat = np.cov(data_cen,rowvar=0)      #计算协方差矩阵,每行为一个样本
    eigVals, eigVects = eig(cov_mat)
    print(eigVects.shape)
    eigValInd = np.argsort(eigVals)
    eigValInd = eigValInd[: -(d + 1) : -1]
    redEigVects = eigVects[:, eigValInd]
    pc_eig = np.dot(data_cen, redEigVects)
    plt.scatter(pc_eig[:,0], pc_eig[:,1], c = labels)
    plt.show()

# 调用sk-learn库做PCA(内部也是用的SVD))
def pac_sk():
    pca = PCA(n_components=2)   #降到2维
    pca.fit(data_cen)                  #训练
    pc_sk=pca.fit_transform(data_cen)   #降维后的数据
    plt.scatter(pc_sk[:,0], pc_sk[:,1], c = labels)
    plt.show()

pca_svd()
pca_eig()
pac_sk()

效果图:

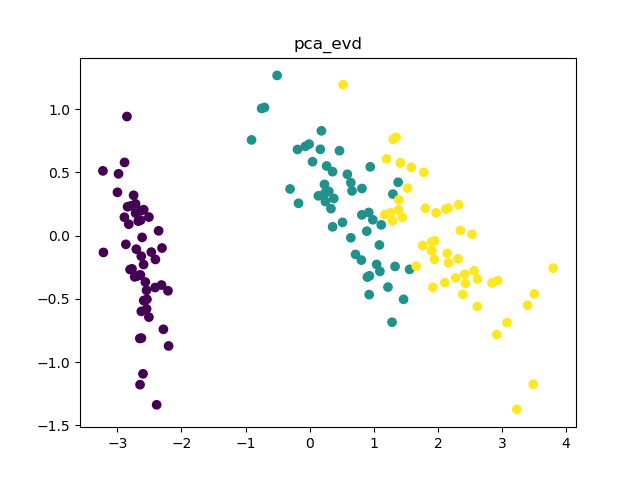
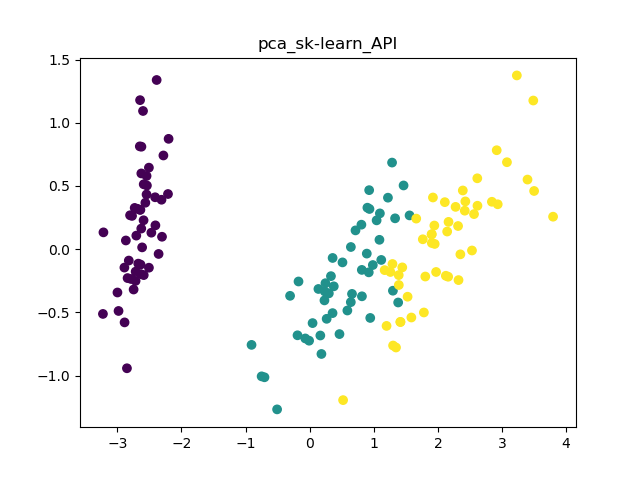
4.详细理论知识传送门

以下是我学习过程中看的几篇高质量文章

PCA SVD基础理论讲解

SVD ( 捎带在PCA中的应用也讲了一点 )

推导SVD和EVD做PCA的等价性