Scipy 学习第3篇：数字向量的距离计算

计算两个数字向量u和v之间的距离函数

1，欧氏距离（Euclidean distance）

在数学中，欧几里得距离或欧几里得度量是欧几里得空间中两点间“普通”（即直线）距离。使用这个距离，欧氏空间成为度量空间。计算公式为

二维空间中的欧氏距离：

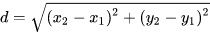
三维空间中的欧式距离：

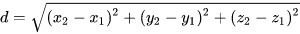
n维空间中的欧式距离：

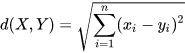
x = [1, 0, 0]
y = [0, 1, 0]
dis = distance.euclidean(x, y)

2，曼哈顿距离（Manhattan／cityblock distance）

曼哈顿距离（Manhattan Distance）用以标明两个点在标准坐标系上的绝对轴距总和。曼哈顿距离的命名原因是从规划为方型建筑区块的城市（如曼哈顿）间，最短的行车路径而来（忽略曼哈顿的单向车道以及只存在于3、14大道的斜向车道）。任何往东三区块、往北六区块的的路径一定最少要走九区块，没有其他捷径。计算公式为：

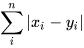
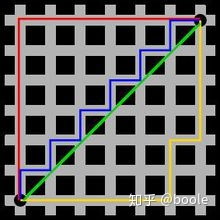
如下图所示，红色表示曼哈顿距离，蓝色和黄色代表等价的曼哈顿距离。

x = [5, 3, 9]
y = [0, 1, 6]
dis = distance.cityblock(x, y)

3，坎贝拉距离（Canberra distance）

Canberra 距离是用来衡量两个向量空间的居间，是Manhattan 距离的加权版本，Canberra 距离已被用作比较排名列表和计算机安全中的入侵检测的测量。

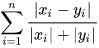
x = [1, 2, 0]
y = [0, 1, 0]
dis = distance.canberra(x, y)

4，切比雪夫距离（Chebyshev distance）

切比雪夫距离（Chebyshev distance）是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。以数学的观点来看，切比雪夫距离是由一致范数（uniform norm）（或称为上确界范数）所衍生的度量，也是超凸度量（injective metric space）的一种。计算公式为

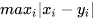
x = [5, 3, 9]
y = [0, 1, 6]
dis = distance.chebyshev(x, y)

5，相关系数距离（Correlation distance）

相关系数距离是1与相关系数的差，相关系数的定义为

常见的Pearson相关性系数即为

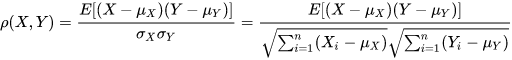
Pearson相关距离为

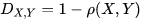
x = [5, 3, 9]
y = [0, 1, 6]
dis = distance.correlation(x, y)

6，余弦相似度距离（Cosine distance）

余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1，而其他任何角度的余弦值都不大于1；并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。余弦相似度通常用于正空间，因此给出的值为0到1之间。

余弦相似度定义来自于欧几里得点积，点积定义如下

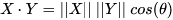
余弦相似度为：

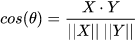
余弦相似度距离为1与余弦相似度的差

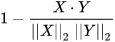
x = [5, 3, 9]
y = [0, 1, 6]
dis = distance.cosine(x, y)

8，闵可夫斯基距离（Minkowski distance）

闵氏距离不是一种距离，而是一组距离的定义，将以下形式的距离都定义为Minkowski distance。

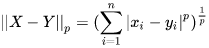 或 

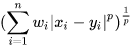
当  时，就是曼哈顿距离 当  时，就是欧氏距离 当  时，就是切比雪夫距离

x = [2, 0, 0]
y = [0, 1, 0]
dis = distance.minkowski(x, y, 2)

9，标准欧式距离（standardized Euclidean distance）

标准化欧氏距离是针对简单欧氏距离的缺点（量纲差异）而作的一种改进方案，标准化方法为

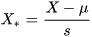
变换后标准欧式距离为

x = [1, 0, 0]
y = [0, 1, 0]
s = [0.1, 0.1, 0.1]
dis = distance.seuclidean(x, y, s)

10，平方欧式距离（squared Euclidean distance）

平方欧式距离是简单欧式距离每一项的平方，公式如下

x = [1, 0, 0]
y = [0, 1, 0]
dis = distance.sqeuclidean(x, y)

11，加权闵可夫斯基距离（Minkowski distance）

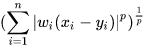
x = [1, 0, 0]
y = [0, 1, 0]
dis = distance.wminkowski(x, y, 2, np.ones(3))

12，Bray-Curtis 相异度

Bray-Curtis 相异度（Bray-Curtis dissimilarity）是生态学中用来衡量不同样地物种组成差异的测度，计算公式为：

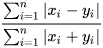
x = [1, 2, 0]
y = [0, 1, 0]
dis = distance.braycurtis(x, y)

参考文档：

scipy.spatial.distance

机器学习常用距离的定义和计算