利用CORDIC算法计算三角函数

这里主要先介绍如何利用CORDIC算法计算固定角度\(\phi\)的\(cos(\phi)\)、\(sin(\phi)\)值。参考了这两篇文章[1]、[2]。

一般利用MATLAB计算三角函数时，用\(cos\)举例，只需要输入相应的\(cos(\phi)\)便自动计算出来了。但是如果是硬件处理或者没有那么方便的函数时，该如何计算\(cos(\phi)\)的值呢？

有一种最傻瓜的方式是用rom存储\(0^o\)到\(90^o\)所有的余弦值，然后用查表的方法计算，但随着精度要求的提升，需要存储的值会越来越多，这是不合适的。那么有没有一种用较少资源且能较快计算出高精度三角函数值的方法呢？有！这就是CORDIC算法可以做的事，算法不难，有一点三角函数和移位运算的基础就能看懂了，核心思想就是把乘法运算变成移位运算。下面来仔细讲解。

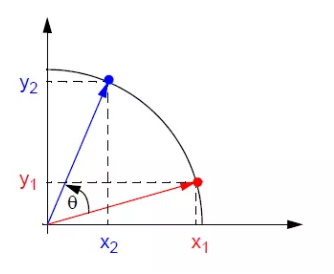
首先引入一个在圆上的坐标旋转公式（不一定单位圆）

\[\begin{cases}
x_2 = x_1cos\theta - y_1sin\theta \\
y_2 = x_1sin\theta + y_1cos\theta \tag{1}\\
\end{cases}
\]

那么如何求\(cos\phi\)和\(sin\phi\)呢？我们可以看出，如果让初始坐标\((x_1, y_1)\)取\(x\)轴一个特定的位置，最后使其旋转\(\phi^o\)到坐标\((x_n,y_n)\)处，且满足\(\sqrt{x_n^2 + y_n^2} = 1\)，那么\(cos\phi\)不就等于\(x_n\)，\(sin\phi\)不就等于\(y_n\)了。这是后话，我们继续看式\((1)\)，\((1)\)也可以写成：

\[\begin{cases}
x_2 = cos\theta(x_1 - y_1tan\theta) \\
y_2 = cos\theta(y_1 + x_1tan\theta)\tag{2} \\
\end{cases}
\]

由于对\((x_2, y_2)\)相当于同乘了一个常数\(cos\theta\)，我们先不看它，不影响旋转角度，得到：

\[\begin{cases}
x_2 = x_1 - y_1tan\theta \\
y_2 = y_1 + x_1tan\theta \tag{3} \\
\end{cases}
\]

---

一：乘法变移位

之前说的我们要把乘法运算变成位移运算，所以我们找到\(tan\theta\)与\(2^{-i}\)之间的对应关系，注意由于是变成移位操作，所以对应旋转的角度也是几个固定的值，但是通过旋转这几个固定的角度，旋转\(i\)次，最终也一定能转到我们需要的角度\(\phi\)上(\(-99.7^o\le\phi \le 99.7^o\))。

于是把\((3)\)再改写为：

\[\begin{cases}
x(i+1) = x(i) - d(i)y(i)2^{-i} \\
y(i+1) = y(i) + d(i)x(i)2^{-i}\tag{4}
\end{cases}
\]

这样，旋转\(\theta^o\)就变成了移位、相加的操作。注意\(d(i) = ±1\)表示旋转的逆、顺时针。

比如要旋转\(\phi = 66^o\)，可以先转\(+45^o\)；\(45^o < 66^o\)，再转\(+26.565^o\)；\(45^o+26.565^o \ge 66^o\)，再转\(-14.036^o \cdots\)，最终会逼近\(66^o\)。而整个运算仅仅进行了\(2^{-0}、2^{-1}、2^{-2} \cdots\)移位操作和加法操作。

---

二：cos累乘项

现在考虑把\(cos\theta\)加回去，回到\((2)\)，且考虑旋转方向\(d_i\)和旋转角度\(\theta_i\)，得到：

\[\begin{cases}
x_2 = cos\theta_1(x_1 - d_1y_1tan\theta_1) \\
y_2 = cos\theta_1(y_1 + d_1x_1tan\theta_1)\tag{5.1} \\
\end{cases}
\]

进行下一次迭代(旋转)，得到：

\[\begin{align}
x_3 &= cos\theta_2(x_2 - d_2y_2tan\theta_2) \\
&= cos\theta_2(cos\theta_1(x_1 - d_1y_1tan\theta_1)- d_2cos\theta_1(y_1 + d_1x_1tan\theta_1)tan\theta_2) \\
&= cos\theta_1cos\theta_2(x_1 - d_1y_1tan\theta_1 - d_2y_1tan\theta_2 - d_2d_1x_1tan\theta_1tan\theta_2)
\end{align} \\
\]

\[\begin{align}
y_3 &= cos\theta_2(y_2 + d_2x_2tan\theta_2) \\
&= cos\theta_2(cos\theta_1(y_1 + d_1x_1tan\theta_1) + d_2cos\theta_1(x_1 - d_1y_1tan\theta_1)tan\theta_2) \tag{5.2}\\
&= cos\theta_1cos\theta_2(y_1 + d_1x_1tan\theta_1 + d_2x_1tan\theta_2 - d_2d_1y_1tan\theta_1tan\theta_2)
\end{align}
\]

可以看到每次旋转都可以提取出\(cos\theta_i\)。\(tan\theta_i\)已经用移位替代了。接下来只用计算\(\prod_{i=1}^{N}cos\theta_i\)就行了，且\(\prod_{i=1}^{N}cos\theta_i\)只跟迭代次数有关，确定了迭代次数后，可以预先把\(\prod_{i=1}^{N}cos\theta_i\)算出来。

---

三：累计旋转角度与旋转方向

现在考虑最后一个问题，如何确定每次迭代的旋转方向\(d_i\)呢？其实定义一个累计旋转角度\(z_i\)

\[z_{i + 1} = z_i -d_i\theta_i = z_i -d_i2^{-i} \tag{6}
\]

令\(z_1\)等于目标角度值，然后每次迭代作个判断就好，如果\(z_i > 0\)，说明当前旋转还没转到目标角度，\(d_{i+1} = 1\)；如果\(z_i < 0\)，说明当前旋转超过了目标角度，\(d_{i+1} = -1\)。

当我们最终转到了目标角度\(\phi\)时，比如\(\phi = 66^o\)，可以此时\(z_i\)已经很小趋近于零了。

另外，在作比较判断时，单次旋转角度\(\theta_i\)则还是需要通过查一次\(arctan(2^{-i})\)表得到，但这个表比起文章开头说的傻瓜式查表要小太多了。

---

四：计算cos和sin值

进行差不多十多次迭代，最后趋近到所需旋转角度\(\phi\)时，最后一个坐标可由如下公式计算：

\[\begin{cases}
x(n) = \frac{1}{\prod_{i=1}^n cos\theta_i}(x(1)cosz_1 - y(1)sinz_1 \\
y(n) = \frac{1}{\prod_{i=1}^n cos\theta_i}(y(1)cosz_1 + x(1)sinz_1 \tag{7}
\end{cases}
\]

关于公式\((6)\)是如何通过公式\((2)(3)(4)(5)\)推出来的，暂时还不太理解。但是我们从公式\((6)\)可以看出，当我们设置初始坐标\((x_1, y_1) = (\prod_{i=1}^n cos\theta_i, 0)\)，再另初始累计旋转角度\(z_1 = \phi\)时：

\[\begin{cases}
cos\phi = x(n) \\
sin\phi = y(n) \tag{8}
\end{cases}
\]

这样就只用通过\((4)(6)\)的移位、相加、一次查表，再迭代十多次，就能计算\(cos\phi\)和\(\sin\phi\)值啦！

其实用CORDIC算法还能计算arctan、sinh、cosh等值，以后学习了再来补充进阶版。

---

### 五：完整MATLAB代码

clc, clear, close all;

%% 初始计算cos累乘值
N = 16; % 设置迭代次数16次
Nprod(1) = 1;
for i = 1 : N
    Nprod(i + 1) = Nprod(i) * cos(atan(2^(-(i - 1))));
end

%% Cordic算法计算cos、sin值
x(1) = Nprod(N); % 横坐标初始值赋为cos累乘值，公式(7)
y(1) = 0; % 纵坐标初始值赋为0，公式(7)
z(1) = 66 / 180 * pi; %目标旋转角度值，66°，注意转化成弧度值
d(1) = 1; %旋转方向，初始肯定为1

for i = 1 : N
    x(i + 1) = x(i) - d(i) * y(i) * 2^(-(i - 1)); %移位运算，公式(4)
    y(i + 1) = y(i) + d(i) * x(i) * 2^(-(i - 1)); %移位运算，公式(4)
    z(i + 1) = z(i) - d(i) * atan(2^(-(i - 1))); %计算累计旋转角度，查一次表，公式(6)
    if z(i + 1) >= 0 % 判断下一次的旋转方向
        d(i + 1) = 1;
    else
        d(i + 1) = -1;
    end
end

COS = x(N) % 输出cos66的值
SIN = y(N) % 输出sin66的值

---

六：参考文章

[1]：https://mp.weixin.qq.com/s/c4oro0bOhdDUmBt0yyLpTA

[2]：https://blog.csdn.net/qq_39210023/article/details/77456031