NOIP复习赛20161117

题目链接：http://files.cnblogs.com/files/candy99/%E9%A2%98%E7%9B%AE1117.pdf

---

A

n个等比数列求和公式(都感觉数列忘光了)

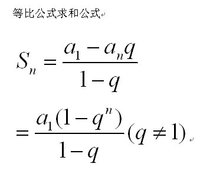
%1e9+7要用逆元

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
typedef long long ll;
const int MOD=1e9+;
int n,m;
ll powMod(ll a,int b){
    ll ans=;
    for(;b;b>>=,a=(a*a)%MOD)
        if(b&) ans=(ans*a)%MOD;
    return ans;
}
void exgcd(ll a,ll b,ll &d,ll &x,ll &y){
    if(b==) {d=a;x=;y=;}
    else {exgcd(b,a%b,d,y,x);y-=(a/b)*x;}
}
ll inv(ll a,ll n){
    ll d,x,y;
    exgcd(a,n,d,x,y);
    return d==?(x+n)%n:-;
}
int main(){
    scanf("%d%d",&n,&m);
    ll ans=m;
    for(int i=;i<=n;i++){
        ll p=powMod(i,m);
        ll tmp=i*(p-)%MOD*inv(i-,MOD)%MOD;
        ans=(ans+tmp)%MOD;
    }
    printf("%lld",ans);
}

---

B

poj two缩水版，连直径都不用求，求从1开始最长路径

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=5e4+;
int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-; c=getchar();}
    while(c>=''&&c<=''){x=x*+c-''; c=getchar();}
    return x*f;
}
int n,u,v,w;
struct edge{
    int ne,v,w;
}e[N<<];
int h[N],cnt=;
void ins(int u,int v,int w){
    cnt++;
    e[cnt].v=v; e[cnt].w=w; e[cnt].ne=h[u]; h[u]=cnt;
    cnt++;
    e[cnt].v=u; e[cnt].w=w; e[cnt].ne=h[v]; h[v]=cnt;
}
int f[N],sum=;
void dp(int u,int fa){
    for(int i=h[u];i;i=e[i].ne){
        int v=e[i].v,w=e[i].w;
        if(v==fa) continue;
        dp(v,u);
        f[u]=max(f[u],f[v]+w);
    }
}
int main(){
    n=read();
    for(int i=;i<=n-;i++) u=read(),v=read(),w=read(),ins(u,v,w),sum+=w*;
    dp(,);
    printf("%d",sum-f[]);
}

---

C

【问题背景】

zhx和妹子们玩数数游戏。

【问题描述】

仅包含4或7的数被称为幸运数。

一个序列的子序列被定义为从序列中删去若干个数，剩下的数组成的新序列。两个子序列被定义为不同的当且仅当其中的元素在原始序列中的下标的集合不相等。对于一个长度为N的序列，共有2^N个不同的子序列。（包含一个空序列）。

一个子序列被称为不幸运的，当且仅当其中不包含两个相同的幸运数。

对于一个给定序列，求其中长度恰好为K的不幸运子序列的个数，答案mod 10^9+7输出。

【输入格式】

第一行两个正整数N，K，表示原始序列的长度和题目中的K。

接下来一行N个整数a_i，表示序列中第i个元素的值。

【输出格式】

仅一个数，表示不幸运子序列的个数。（mod 10^9+7）

【样例输入】

3 2

1 1 1

【样例输出】

3

【样例输入】

4 2

4 7 4 7

【样例输出】

4

【样例解释】

对于样例1，每个长度为2的子序列都是符合条件的。

对于样例2，4个不幸运子序列元素下标分别为：{1, 2}, {3, 4}, {1, 4}, {2, 3}。注意下标集{1, 3}对应的子序列不是“不幸运”的，因为它包含两个相同的幸运数4.

---

卡读题啊

是序列不是字符串，只含4或7是幸运数字，有两个相同的幸运数字是不幸运序列

搜了题解

幸运数字大约2^10个，可以预处理出来，直接构造不幸运数列

ans=Σ(0<=i<=k) C(n1,i)*f(n2,k-i)

n1是不幸运数字数量，n2是幸运数字数量

f[i][j]表示前i个幸运数字选j个的方案数，一个幸运数字只能选一个，所以需要DP

组合数也需要逆元

PS：构造幸运数字的dfs少写了一层。。。。。。。查了好久

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
typedef long long ll;
const int N=1e5+,M=1e3+;
const int MOD=1e9+;
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int n,k,a,n1,n2;
ll luc[M],cnt=,sum[M];
void dfs(int d,ll now){
    if(now) luc[++cnt]=now;
    if(d==) return;
    dfs(d+,now*+);
    dfs(d+,now*+);
}
ll f[N],c[N];
void exgcd(ll a,ll b,ll &d,ll &x,ll &y){
    if(b==) {d=a;x=;y=;}
    else {exgcd(b,a%b,d,y,x);y-=(a/b)*x;}
}
ll inv(ll a,ll n){
    ll d,x,y;
    exgcd(a,n,d,x,y);
    return d==?(x+n)%n:-;
}
void dp(){
    f[]=;
    for(int i=;i<=cnt;i++) if(sum[i]>=)
        for(int j=i;j>=;j--)
            f[j]=(f[j]+f[j-]*sum[i]%MOD)%MOD;

    c[]=;
    for(int i=;i<=n1;i++)
        c[i]=c[i-]*(n1-i+)%MOD*inv(i,MOD)%MOD;
}
int main(){
    n=read();k=read();
    n1=n;
    dfs(,);
    sort(luc+,luc++cnt);
    for(int i=;i<=n;i++){
        a=read();
        int p=lower_bound(luc+,luc++cnt,a)-luc;
        if(luc[p]==a){
            sum[p]++;    //sum[p]==1  regard as unlucky
            if(sum[p]==) n2++,n1-=;
            if(sum[p]>) n1--;
        }
    }
    dp();
    ll ans=;
    for(int i=;i<=k;i++) ans=(ans+c[i]*f[k-i]%MOD)%MOD;
    printf("%lld",ans);
}