OpenCASCADE构造一般曲面

eryar@163.com

Abstract. 本文主要介绍常见的曲面如一般柱面（拉伸曲面）、旋转面在OpenCASCADE中的构造方法，由此思考一般放样算法的实现。

Key Words. Common Surface, Extrusion, Revolution

1.Introduction

实体Solid就是由面组成，面中包含几何曲面，常见的几何曲面有平面，柱面，旋转面等。对几何曲面有一些功能要求：如计算指定参数u,v处的点，切线等，即求指定参数u,v处的0阶导数、1阶导数，N阶导数；获取参数空间等。

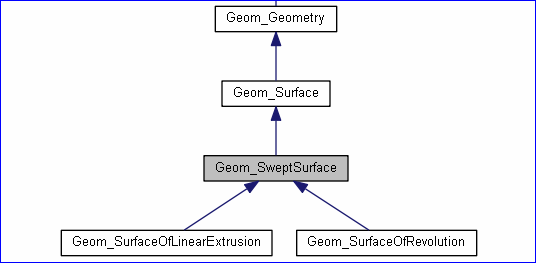
图1. 放样曲面

由类图可以看出，放样曲面Swept Surface有两种形式：Geom_SurfaceOfLinearExtrusion和Geom_SurfaceOfRevolution。一种是线性拉伸成形的曲面，一种是旋转成形的曲面。

图2. 拉伸曲面

如上图1所示，可以将一条曲线沿一方向拉伸一定的距离来构造曲面，被拉伸的曲线称为准线。

图3. 旋转曲面

如上图2所示，将一条曲线绕指定的轴线旋转一定的角度得到一个旋转面。

本文结合OpenCASCADE中源码来说明拉伸曲面及旋转曲面原理。

2.The Surface of Extrusion

OpenCASCADE中线性拉伸曲面的类名为：Geom_SurfaceOfLinearExtrusion，其参数方程如下：

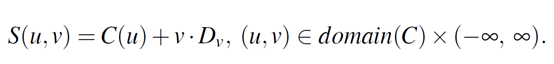
其中参数u的定义域决定准线C(u)的参数范围；参数v的取值范围是无穷的。即拉伸曲面是一个很长的柱面，如果在参数v上不加限制的话。其中一些计算功能代码如下所示：

//! Shift the point along direction to the given distance (theShift)

void Shift(const Standard_Real theShift, gp_Pnt& thePoint) const

{

  thePoint.ChangeCoord() += myDirection.XYZ() * theShift;

}

void GeomEvaluator_SurfaceOfExtrusion::D0(

    const Standard_Real theU, const Standard_Real theV,

    gp_Pnt& theValue) const

{

  if (!myBaseAdaptor.IsNull())

    myBaseAdaptor->D0(theU, theValue);

  else

    myBaseCurve->D0(theU, theValue);

  Shift(theV, theValue);

}

从计算曲面上在指定参数u,v处的点的函数D0()可以看出，先根据参数u计算出准线上的点，再将点沿拉伸方向移动拉伸向量模的距离。

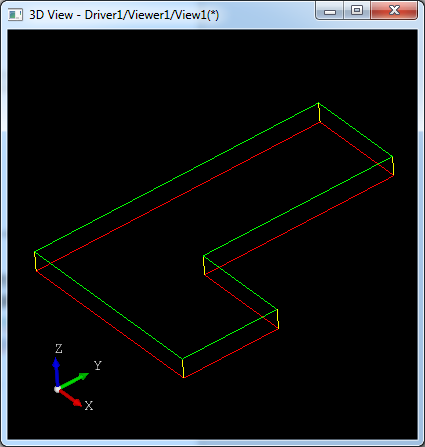
图4. 拉伸多边形

如上图4所示为将多边形准线沿着Z方向拉伸得到一个拉伸曲面。

3.The Surface of Revolution

OpenCASCADE中旋转曲面的类名为：Geom_SurfaceOfRevolution，其参数方程如下：

其中计算旋转曲面上对应参数u,v的点的代码如下：

void GeomEvaluator_SurfaceOfRevolution::D0(

    const Standard_Real theU, const Standard_Real theV,

    gp_Pnt& theValue) const

{

  if (!myBaseAdaptor.IsNull())

    myBaseAdaptor->D0(theV, theValue);

  else

    myBaseCurve->D0(theV, theValue);

  gp_Trsf aRotation;

  aRotation.SetRotation(myRotAxis, theU);

  theValue.Transform(aRotation);

}

根据代码可知，先根据参数v计算曲线上的点，再将点按指定的轴旋转变换。

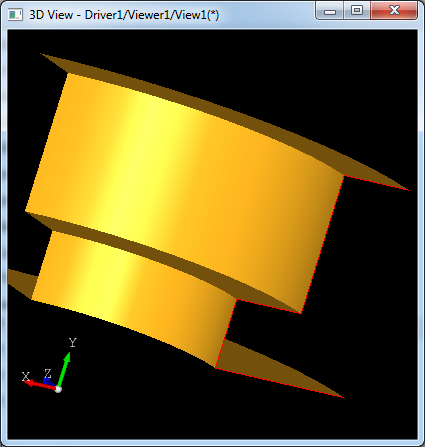
图5. 旋转曲面

如上图5所示，将红色母线绕Y轴旋转90度得到的旋转曲面。线性拉伸曲面和旋转曲面都是特定条件下的放样曲面。拉伸曲面为沿直线放样得到的曲面，旋转曲面是沿圆放样得到的曲面。由此，可以思考一个问题，那就是如何将任意一个曲面沿任意路径来放样构造曲面呢？

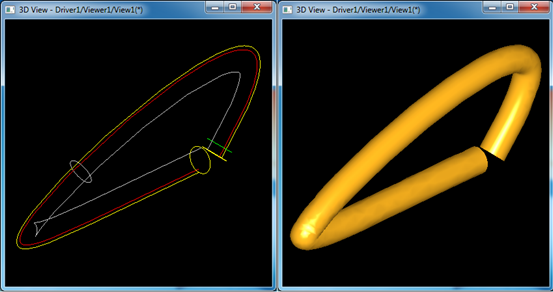
图6. 放样曲面