开地址哈希表（Hash Table）的原理描述与冲突解决

在开地址哈希表中，元素存放在表本身中。这对于某些依赖固定大小表的应用来说非常有用。因为不像链式哈希表在每个槽位上有一个“桶”来存储冲突的元素，所以开地址哈希表需要通过另一种方法来解决冲突。

解决冲突的方法

在开地址哈希表中，解决冲突的方法就是探查这个表，直到找到一个可以放置元素的槽。

例如，插入一个元素时，我们探查槽位直到找到一个空槽，然后将元素插入此槽中。删除或查找一个元素时，我们探查槽位直到定位到该元素或找到一个空槽。如果在找到元素之前找到一个空槽或遍历完所有槽位，那么说明此元素在表中不存在。

我们要做的就是尽可能地减少探查的次数。究竟进行多少次探查后就停止，这主要取决于两件事：哈希表的负载因子和元素均匀分布的程度。

哈希表的负载因子a=n / m，n为元素个数，m为可以散列元素的槽位个数。根据开地址哈希表的定义，n不可能大于m，所以 开地址哈希表的负载因子通常小于或等于1。

假设散列是均匀的，我们能够在一个开地址哈希表中探查的槽位个数将是：1 / （1-a）

举例来说，对于一个处于半满状态的开地址哈希表来说（负载因子为0.5），我们期望能够探查的槽位个数为1/（1-0.5）=2。

下表列示了当哈希表的负载因子趋近于1时（即表完全满时），我们期望探查的槽位数量如何显著增长。在一个对时间特别敏感的应用中，就可以通过增加哈希表的空间（槽位数）来提高探查的效率。

哈希表的性能能否接近于这个规律取决于我们是否能够近似均匀散列，这关键取决于如何选取哈希函数。

一般来说，在开地址哈希表中探查槽位的哈希函数定义为：

h(k,i) = x

其中，k是键，i是到目前为止探查的次数，x是得到的哈希编码。通常情况下，与链式哈希表一样，h会调用一个或多个具有具有相同属性的辅助哈希函数。但在开地址哈希表中，h必须具有一个额外的属性：当i从0增长到m-1(m为哈希表中槽位的个数)时，在第二次访问任何槽位之前，表中所有的槽位都必须访问过一遍；否则，就说明不需要探查所有的槽位就能找到结果。

两种探查方法：线性探查和双散列

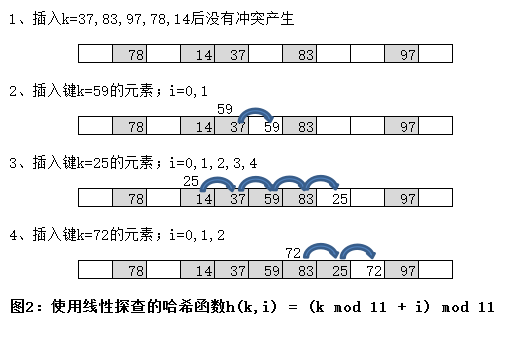
线性探查是开地址哈希表中一种简单的探查方法，探查表中连续的槽位。正式的表述为，如果i大于0，小于m-1(m为表中的槽位个数)，那么一个线性探查方法的哈希函数定义为：

h(k,i) = (h'(k)+i) mod m

函数h'是一个辅助的哈希函数，就像任何哈希函数的选择方法一样，它会尽可能地将元素随机和均匀地分布在表中。比如采用取余法，h'(k)= k mod m。如果将一个元素（k=2998）散列到表（容量m=1000)，所得到的哈希编码为（998+0） mod 1000 =998（当i = 0时)，（998+1） mod 1000 = 999（当i = 1时），（998+2）mod 1000 = 0（当i=2时）...依此类推。也就是说，当要插入一个键k = 2998的元素时，我们会寻找一个空的槽位，首先探查槽位998，然后999，然后0...，依此类推。

线性探查的优点是简单，而且对m没有限制，这样就可以保证所有的槽位最终都可能探查到。遗憾的是，线性探查并不能近似均匀散列。特别是当遇到和种称为基本聚集的情况时，基本聚集会产生很长的探查序列，从而使表变得越来越大。这种过度的探查会降低表的性能。

双散列

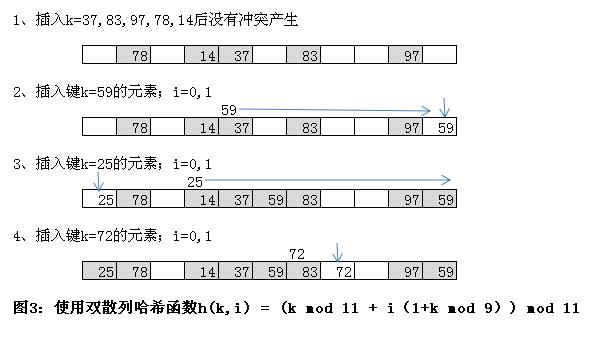
最有效地探查开地址哈希表的方法之一，就是 通过计算两个辅助哈希哈希编码的和 来得到哈希编码。正式的表述为，如果i的大小在0和m之间（m为表中槽位的个数），双散列的哈希函数定义为：

h( k, i ) = (h1(k) + i h2(k)) mod m

函数h1和h2是两个辅助哈希函数，它们与其他的哈希函数一样，也会尽可能地将元素随机和均匀的散列到表中。为了保证第二次访问任何一个槽位之前其他所有的槽位都访问过一遍，我们必须遵循如下规则：一种方法是，m必须是2次幂，让h2返回一个奇数值；另一种方法是选择m为一个素数，h2返回的值在1<= h2(k) <= m-1之间。

通常情况下，令h1(k) = k mod m，h2(k) = 1+(k mod m')，其中m'略小于m，类似等于m-1或m-2。例如，如果哈希表槽位数m=1699（素数），要散列的键k=15385，探查到的槽位为（940+0X113) mod 1699 = 94（当i=0时），以及之后每隔113位置的槽位（随i的增加）。

双散列的优点是，它能够在表中探查并产生较好的元素分布。其缺点是，必须限制m的值，这样才能够保证在一系列探查中访问表中所有槽位之后才会再次探查任何槽位。