[SinGuLaRiTy] 复习模板-数学

【SinGuLaRiTy-1047】 Copyright (c) SinGuLaRiTy 2017. All Rights Reserved.

质因数分解

void solve(int n)
{
    while(n%==)
    {
        printf("%d*",);
        n/=;
    }
    for(int i=;i<=sqrt(n);i+=)
    {
        if(n%i==)
        {
            n/=i;
            printf("%d*",i);
            i-=;
        }
    }
    printf("%d\n",n);
}

欧拉线性筛素数

#define MAXN 100005
#define MAXL 1299710

int prime[MAXN];
int check[MAXL];

int tot=;

void get_prime()
{
    for(int i=;i<MAXL;i++)
    {
          if(!check[i])
            prime[tot++]=i;
          for(int j=;j<tot;j++)
          {
            if(i*prime[j]>MAXL)
                break;
            check[i*prime[j]]=;
            if(i%prime[j]==)
                 break;
          }
    }
}

筛法求欧拉函数(线性)

#include<iostream>
#include<cstdio>  
#define N 40000  
using namespace std;  
int n;
int phi[N+],prime[N+],tot,ans;
bool mark[N+];  
void getphi()
{
   int i,j;
   phi[]=;
   for(i=;i<=N;i++)//相当于分解质因式的逆过程
   {
       if(!mark[i])
       {
           prime[++tot]=i;//筛素数的时候首先会判断i是否是素数。
           phi[i]=i-;//当 i 是素数时 phi[i]=i-1
       }
       for(j=;j<=tot;j++)
       {
          if(i*prime[j]>N)  
              break;
          mark[i*prime[j]]=;//确定i*prime[j]不是素数
          if(i%prime[j]==)//接着我们会看prime[j]是否是i的约数
          {
              phi[i*prime[j]]=phi[i]*prime[j];
              break;
          }
          else  
              phi[i*prime[j]]=phi[i]*(prime[j]-);//其实这里prime[j]-1就是phi[prime[j]]，利用了欧拉函数的积性
       }
   }
}  

Miller-Rabbin素数判定法

#include<cstdlib>
#include<ctime>
#include<cstdio>

using namespace std;

const int count=;

int modular_exp(int a,int m,int n)
{
    if(m==)
        return ;
    if(m==)
        return (a%n);
    long long w=modular_exp(a,m/,n);
    w=w*w%n;
    if(m&)
        w=w*a%n;
    return w;
} 

bool Miller_Rabin(int n)
{
    if(n==)
        return true;
    for(int i=;i<count;i++)
    {
        int a=rand()%(n-)+;
        if(modular_exp(a,n,n)!=a)
            return false;
    }
    return true;
}

int main()
{
    srand(time(NULL));
    int n;
    scanf("%d",&n);
    if(Miller_Rabin(n))
        printf("Probably a prime.");
    else
        printf("A composite.");
    printf("\n");
    return ;
}

倍增求快速幂

typedef long long ll;

ll fast_power(ll a,ll b,ll c)//求a^b%c
{
    ll ans=;
    while(b)
    {
        if (b&)
            ans=ans*a%c;
        else
            ans%=c;
        b>>=;
        a=a*a%c;
    }
    return ans;
}

大数乘法取幂

typedef long long ll

ll qmul(ll x,ll y,ll mod)// 乘法防止溢出,如果p*p不爆LL的话可以直接乘；O(1)乘法或者转化成二进制加法(快速加)
{
    ll ret=;
    while(y)
    {
        if(y&)
            ret=(ret+x)%mod;
        x=x*%mod;
        y>>=;
    }
    return ret;
}

ll qpow(ll a,ll n,ll mod)
{
    ll ret=;
    while(n)
    {
        if(n&)
            ret=qmul(ret,a,mod);
        a=qmul(a,a,mod);
        n>>=;
    }
    return ret;
}

GCD & LCM

LL gcd(LL a,LL b)
{
    return b ? gcd(b,a%b) : a;
}

至于LCM=a*b/GCD，可能会因为a*b过大而爆掉，于是推荐使用LCM=a/GCD*b

Exgcd

求ax=b (mod m) ax+my=b 如果r=gcd(a,m)且b%r==0,则同余方程有解,其最小解为x*(b/r);
ax+by=c 如r=gcd(a,b),则存在x,y,使xa+yb=r;当x+=b,y-=a后仍然成立        
因为xa+yb+ab-ab=r;则(x+b)a+(y-a)b=r

int exgcd(int a,int b,int &x,int &y)
{
     if(b==)
    {
        x=;
        y=;
        return a;
    }
     int r=exgcd(b,a%b,y,x);
     y-=x*(a/b);
     return r;
}

中国剩余定理

设正整数m1,m2,m3...mk两两互素，则同余方程组

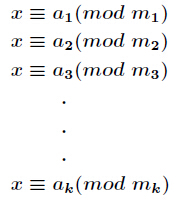
有整数解。并且在模M=m1·m2·...·mk下的解是唯一的，解为

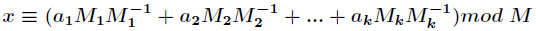
其中，而为模的逆元。

void extend_Euclid(int a,int b,int &x,int &y)
{
    if(b==)
    {
        x=;
        y=;
        return;
    }
    extend_Euclid(b,a%b,x,y);
    int tmp=x;
    x=y;
    y=tmp-(a/b)*y;
}  

int CRT(int a[],int m[],int n)
{
    int M=;
    int ans=;
    for(int i=;i<=n;i++)
        M*=m[i];
    for(int i=;i<=n;i++)
    {
        int x,y;
        int Mi=M/m[i];
        extend_Euclid(Mi,m[i],x,y);
        ans=(ans+Mi*x*a[i])%M;
    }
    if(ans<)
        ans+=M;
    return ans;
}  

Catalan数

f[]=;
for(int i=;i<=n;i++)
    f[i]=f[i-]*(*i-)/(i+);

Catalan数有许多神奇的性质，这是一篇总结的比较精炼的文章。《Catalan数——卡特兰数》

康托展开式

int  fac[] = {,,,,,,,,}; //i的阶乘为fac[i]
// 康托展开-> 表示数字a是 a的全排列中从小到大排，排第几
// n表示1~n个数  a数组表示数字。
int kangtuo(int n,char a[])
{
    int i,j,t,sum;
    sum=;
    for( i=;i<n;++i)
    {
        t=;
        for(j=i+;j<n;++j)
            if(a[i]>a[j])
                ++t;
        sum+=t*fac[n-i-];
    }
    return sum+;
}  

有啥用？它可以应用于哈希表中空间压缩。在码某些搜索题时，将VIS数组量压缩。比如:八数码、魔板。

求乘法逆元

exgcd，老熟人了。

/*
求解ax+by=gcd(a,b)，亦即ax≡1(mod b)。函数返回值是a,b的最大公约数，而x即a的逆元。
注意a, b不能写反了。
*/
int x,y;
int extgcd(int a,int b,int &x,int &y)
{
    if(b==)
    {
        x=;
        y=;
        return a;
    }
    int gcd=exgcd(b,a%b, x, y);
    int tmp=x;
    x=y;
    y=tmp-(a/b)*y;
    return gcd;
}  

N的全排列

#include<iostream>

using namespace std;

void swap(int &a,int &b)
{
    int temp=a;
    a=b;
    b=temp;
}

void pai_xu(int a[],int m,int n)
{
    if(m==n)
        {
        for(int i=;i<=n;i++)
            cout<<a[i];
        cout<<endl;
    }
    else
        for(int i=m;i<=n;i++)
                {
            swap(a[i],a[m]);
            pai_xu(a,m+,n);
            swap(a[i],a[m]);
        }
}

int main()
{
    int n,m=,a[];
    cin>>n;
    for(int i=;i<=n;i++)
        a[i]=i;
    pai_xu(a,m,n);
    return ;
}

N的R排列

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cmath>

using namespace std;

bool b[]={};
int total=,a[]={};

bool pd(int x,int y)
{
     int k=,i=x+y;
     while(k<=sqrt(i)&&i%k!=)
         k++;
     if(k>sqrt(i))
         return ;
     else
         return ;
}

int print()
{
    total++;
    cout<<total<<" "<<endl;
    for(int i=;i<=;i++)
        cout<<a[i]<<" ";
    cout<<endl;
}

int search(int t)
{
    for(int i=;i<=;i++)
        if(pd(a[t-],i)&&(!b[i]))
        {
            a[t]=i;
            b[i]=;
            if(t==)
            {
                if(pd(a[],a[]))
                    print();
            }
            else
                search(t+);
            b[i]=;
        }
}

int main()
{
    search();
    cout<<total<<endl;
    return ;
}

有重复元素的全排列

void fun(int n,char chars[],int flag) {
    if(flag==n-) {
        for(int i=;i<n;i++) cout<<chars[i];
        cout<<endl;
        return;
    }
    for(int i=flag;i<n;i++) {
        if(chars[i]!=chars[flag]||i==flag){//若两个元素不相等或者两个元素的下标相同的时候才调用
            swap(chars[i],chars[flag]);
            fun(n,chars,flag+);
            swap(chars[i],chars[flag]);
        }
    }
}  

第一类Stirling数

定理：第一类Stirling数s(p,k)计数的是把p个对象排成k个非空循环排列的方法数。

证明：把上述定理叙述中的循环排列叫做圆圈。递推公式为：

s(p,p)=1 (p>=0)    有p个人和p个圆圈，每个圆圈就只有一个人

s(p,0)=0 (p>=1)    如果至少有1个人，那么任何的安排都至少包含一个圆圈

s(p,k)=(p-1)*s(p-1,k)+s(p-1,k-1)

设人被标上1,2,.....p。将这p个人排成k个圆圈有两种情况。第一种排法是在一个圆圈里只有标号为p的人自己，排法有s(p-1,k-1)个。第二种排法中，p至少和另一个人在一

个圆圈里。这些排法可以通过把1,2....p-1排成k个圆圈再把p放在1,2....p-1任何一人的左边得到，因此第二种类型的排法共有(p-1)*s(p-1,k)种排法。

在证明中我们所做的就是把{1,2,...,p}划分到k个非空且不可区分的盒子，然后将每个盒子中的元素排成一个循环排列。

long long s[maxn][maxn];//存放要求的第一类Stirling数
const long long mod=1e9+;//取模  

void init()//预处理
{
    memset(s,,sizeof(s));
    s[][]=;
    for(int i=;i<=maxn-;i++)
        for(int j=;j<=i;j++)
    {
        s[i][j]=s[i-][j-]+(i-)*s[i-][j];
        if(s[i][j]>=mod)
            s[i][j]%=mod;
    }
}  

第二类Stirling数

定理：第二类Stirling数S(p,k)计数的是把p元素集合划分到k个不可区分的盒子里且没有空盒子的划分个数。

证明：元素在拿些盒子并不重要，唯一重要的是各个盒子里装的是什么，而不管哪个盒子装了什么。

递推公式有：S(p,p)=1 (p>=0)         S(p,0)=0  (p>=1)         S(p,k)=k*S(p-1,k)+S(p-1,k-1)   (1<=k<=p-1)。考虑将前p个正整数，1，2，.....p的集合作为要被划分的集合，把

{1,2,.....p}分到k个非空且不可区分的盒子的划分有两种情况：

(1)那些使得p自己单独在一个盒子的划分，存在有S(p-1,k-1)种划分个数

(2)那些使得p不单独自己在一个盒子的划分，存在有 k*S(p-1,k)种划分个数

考虑第二种情况，p不单独自己在一个盒子，也就是p和其他元素在一个集合里面，也就是说在没有放p之前，有p-1个元素已经分到了k个非空且不可区分的盒子里面（划

分个数为S(p-1,k），那么现在问题是把p放在哪个盒子里面呢，有k种选择，所以存在有k*S(p-1,k)。

long long s[maxn][maxn];//存放要求的Stirling数
const long long mod=1e9+;//取模  

void init()//预处理
{
    memset(s,,sizeof(s));
    s[][]=;
    for(int i=;i<=maxn-;i++)
        for(int j=;j<=i;j++)
    {
        s[i][j]=s[i-][j-]+j*s[i-][j];
        if(s[i][j]>=mod)
            s[i][j]%=mod;
    }
}  

注意：要用long long类型，当元素个数>20，就超int类型了。

扩展：k! *S(p,k) 计数的是把p元素集合划分到k个可区分的盒子里且没有空盒子的划分个数。

组合数

//组合数打表模板,适用于N<=3000
//c[i][j]表示从i个中选j个的选法。
long long C[N][N];
void get_C(int maxn)
{
    C[][] = ;
    for(int i=;i<=maxn;i++)
    {
        C[i][] = ;
        for(int j=;j<=i;j++)
            C[i][j] = C[i-][j]+C[i-][j-];
        //C[i][j] = (C[i-1][j]+C[i-1][j-1])%MOD;
    }
}

LUCAS定理

long long F[];
void init(long long p)
{
    F[] = ;
    for(int i = ;i <= p;i++)
        F[i] = F[i-]*i % ();
}
long long inv(long long a,long long m)
{
    if(a == )return ;
    return inv(m%a,m)*(m-m/a)%m;
}
long long Lucas(long long n,long long m,long long p)
{
    long long ans = ;
    while(n&&m)
    {
        long long a = n%p;
        long long b = m%p;
        if(a < b)return ;
        ans = ans*F[a]%p*inv(F[b]*F[a-b]%p,p)%p;
        n /= p;
        m /= p;
    }
    return ans;
}  

容斥原理

这个怎么打板呢？难道搞一道容斥的题？还是偷偷懒附个链接吧：

《算法中的容斥原理》

Time: 2017-11-05