HDU6166-Senior Pan-Dijkstra迪杰斯特拉算法(添加超源点,超汇点)+二进制划分集合-2017多校Team09

学长好久之前讲的，本来好久好久之前就要写题解的，一直都没写，懒死_(:з」∠)_

Senior Pan

Time Limit: 12000/6000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 1332    Accepted Submission(s): 533

Problem Description

Senior Pan fails in his discrete math exam again. So he asks Master ZKC to give him graph theory problems everyday.
The task is simple : ZKC will give Pan a directed graph every time, and selects some nodes from that graph, you can calculate the minimum distance of every pair of nodes chosen in these nodes and now ZKC only cares about the minimum among them. That is still too hard for poor Pan, so he asks you for help.

 

Input

The first line contains one integer T, represents the number of Test Cases.1≤T≤5.Then T Test Cases, for each Test Cases, the first line contains two integers n,m representing the number of nodes and the number of edges.1≤n,m≤100000
Then m lines follow. Each line contains three integers xi,yi representing an edge, and vi representing its length.1≤xi,yi≤n,1≤vi≤100000
Then one line contains one integer K, the number of nodes that Master Dong selects out.1≤K≤n
The following line contains K unique integers ai, the nodes that Master Dong selects out.1≤ai≤n,ai!=aj

 

Output

For every Test Case, output one integer: the answer

 

Sample Input

1

5 6

1 2 1

2 3 3

3 1 3

2 5 1

2 4 2

4 3 1

3

1 3 5

 

Sample Output

Case #1: 2

Source

2017 Multi-University Training Contest - Team 9

题意就是一个有向图，给出一个查询的集合，求出集合中任意两点之间的最短距离。

这个题很神奇呀，一开始没明白什么意思，感觉好难啊，懂了之后就感觉有点水。。。

这个题用迪杰斯特拉算法+二进制划分集合就可以写出来。

为什么用迪杰斯特拉呢，迪杰斯特拉算法是解决单源最短路径问题呀，这个题可以自己加上源点和汇点，然后就可以使用迪杰斯特拉算法啦。

为什么要这么做呢？因为这样可以节省时间什么的呀，具体下面哔哔出来。。。

因为是从给出的查询集合中任意两点的最短路径，但是不确定是任意的哪两个点呀。如果一个一个枚举的话，后果不堪设想呀。。。

所以就可以通过把要查询的点分成两个集合，一部分作为起点集合，一部分作为终点集合。然后起点的集合与源点连接，终点的集合与汇点连接，边权都设为0就可以了。

通过这种操作就可以跑一遍迪杰斯特拉找出来好几个任意两点的最短距离，这样比一个一个枚举快多了。然后起点和终点互换再跑一次就可以了。

至于迪杰斯特拉算法，emnnnn，该算法是解决单源最短路径问题的，采用了贪心的思想，

每次都是查找与该点距离最近的点，就是因为这样，该算法不能用来解决存在负权边的图。

迪杰斯特拉算法的原理什么的，传送门:1.哈哈哈 2.咯咯咯 3.嘎嘎嘎 4.呵呵呵 5.蛤蛤蛤(反正不想写。。。)

好啦，进行下一步(ﾉﾟ▽ﾟ)ﾉ怎么分这个起点集合和终点集合呢？怎么才能做到把所有的都考虑到呢？二进制划分集合就登场啦，噔噔噔噔~

因为对于任意两个点，这两个点是不同的，那么对应的二进制表示至少有一位是不同的，所以至少会有一次可以把他们分到正确的集合当中，得到正确的结果，其他的都会比结果的数值要大。

举个例子，拿样例来说，图就是这样的

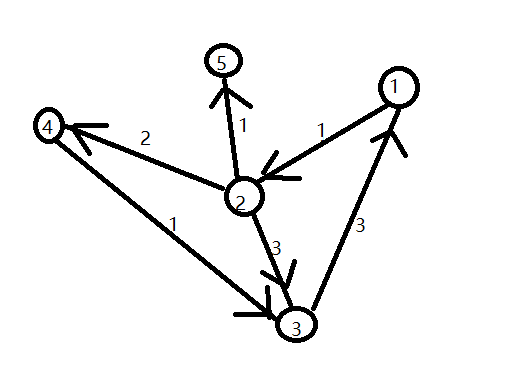
样例是找1,3,5中任意两点的最短距离。

1--->001

3--->011

5--->101

首先按最低位分类，最低位都是1，所以1,3,5全都在一个集合里，因为只有起点集合或者终点集合，所以最短路径都为INF(不存在就是无限大)。

然后再按次低位分类，就是1和5在一个集合里，3在一个集合里，假设1和5在起点的集合里，简化出来的路径就是这样的

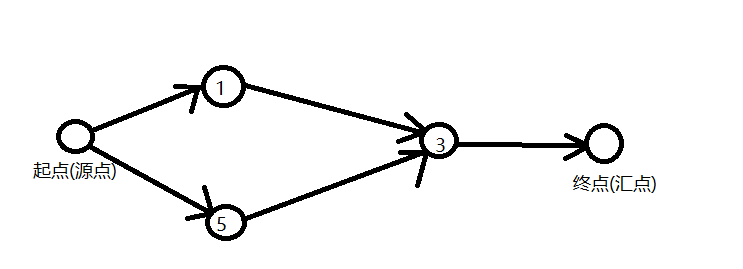
通过找从源点到汇点的最短距离，就把从1到3和从5到3的最短路径通过一次迪杰斯特拉就跑出来了。

从源点到1和5最短距离相同，然后再从1到3或者从5到3，看第一个图，下一步要走的就是判断从1到2和从5到2哪个最短，路径不存在的距离是INF(无限大)然后继续，就是迪杰斯特拉，贪心思想。

(下面的过程中的那些点就不仔细说了，自己看第一个图自己想想迪杰斯特拉就可以了〒▽〒)

然后再按下一位分类就是1和3在一个集合中，5在一个集合中，然后假设1和3在起点集合中，5在终点集合中，和上面操作一样。

最后找出来的最短距离为2，就是结果。

如果数据很多，通过分起点和终点集合就可以大大的节省时间。

根据题意，数据最大是100000，100000(十进制) = 11000011010100000(二进制)

对应的二进制有17位，所以最多也是算17*2次，那省时是大大的~

就是这样，自己太菜，直接贴官方的代码吧。。。

代码:

 /*有向图，给出询问集合，求出集合中的点，两两之间的最短距离
 因为边权都是正的，所以用的Dijkstra算法求最短路
 开一个超源0，用长度为0的边连接到各个起点，在把每个终点用长度为0的边连接到超汇n+1
 这样0到n+1的最短路就是从所有的起点到所有的终点路径中最短的
 所以要想办法把真正的最短答案的起点分到起点集合，最优终点放到终点集合，
 然后起点终点互换，再做一次即可。
 */
 #include <stdio.h>
 #include <algorithm>
 #include <iostream>
 #include <queue>
 using namespace std;

 #define N 100010
 #define INF 0x3f3f3f3f3f3f3f3fLL
 #define LL long long
 #define p E[i].x
 #define bit(x) (1<<(x))

 using namespace std;

 struct node{
     int x;
     LL v;
     bool operator<(const node &tmp)const{       //定义结构体，sort时按v大的优先。
         return v>tmp.v;
     }
 };

 priority_queue<node> q;  

 struct edge{      //结构体
     int x,to,v;
 }E[N<<];

 int n,m,totE,g[N],X[N],Y[N],Z[N],a[N];
 LL dist[N];
 bool v[N];

 void addedge(int x,int y,int v){ //存边
     E[++totE] = (edge){y,g[x],v}; g[x] = totE;
 }

 LL calc_dist(int S,int T){    //迪杰斯特拉算法
     for(int i=;i<=n+;i++) dist[i] = INF, v[i] = ;
     dist[S]=;
     q.push((node){S,});
     node tmp;
     while(!q.empty()){
         tmp = q.top(); q.pop();
         int x = tmp.x;
         if(v[x]) continue;
         v[x] = ;
         for(int i=g[x];i;i=E[i].to)
         if(!v[p] && dist[p]>dist[x]+E[i].v){
                 dist[p] = dist[x] + E[i].v;
                 q.push((node){p,dist[p]});
         }
     }
     return dist[T];
 }

 int main(){
     //freopen("in0.txt","r",stdin);
     int T,K,Te = ;
     cin>>T;
     while(T--){
         scanf("%d%d",&n,&m);
         for(int i=;i<=m;i++) scanf("%d%d%d",&X[i],&Y[i],&Z[i]);
         scanf("%d",&K);

         for(int i=;i<=K;i++) scanf("%d",&a[i]);
         LL ans = INF;
         for(int t=;t<;t++){    //将点分成两个集合，一部分为起点，一部分为终点。二进制位数最大为17位，这里取的20，肯定可以。
             totE = ;
         for(int i=;i<=n+;i++) g[i] = ;
         for(int i=;i<=m;i++) addedge(X[i],Y[i],Z[i]);
         for(int i=;i<=K;i++){
             if(a[i]&bit(t)) addedge(,a[i],);//将这些点作为起点集合和源点相连，边权为0
             else addedge(a[i],n+,);//终点集合与汇点相连，边权为0
         }
         ans = min(ans, calc_dist(,n+));
             totE = ;
         for(int i=;i<=n+;i++) g[i] = ;
         for(int i=;i<=m;i++) addedge(X[i],Y[i],Z[i]);
         for(int i=;i<=K;i++){
             if((a[i]&bit(t))==) addedge(,a[i],);//和上边差不多，只是这次作为终点集合与汇点相连
             else addedge(a[i],n+,);//起点集合与源点相连
         }
             ans = min(ans, calc_dist(,n+));   //结果为最短路
         }
         //assert( ans < INF );
         printf("Case #%d: %lld\n",++Te,ans);
     }
     return ;
 }

 /*迪杰斯特拉算法，运用贪心的算法模式，求解最短路。
 算法解决的是有向图中单个源点到其他顶点的最短路径问题
 主要特点是每次迭代时选择的下一个顶点是标记点之外的距离源点最近的顶点
 */

太菜了(；´д｀)ゞ，个人是这样理解的，错了就打我吧－＝≡ヘ(*・ω・)ノ

_(:з」∠)_ 溜了溜了。。。