python科学计算_scipy_常数与优化

scipy在numpy的基础上提供了众多的数学、科学以及工程计算中常用的模块；是强大的数值计算库；

1. 常数和特殊函数

scipy的constants模块包含了众多的物理常数：

import scipy.constants as C
C.c  #真空中的光速
C.h  #普朗克常数
C.pi #圆周率 

在C.physical_constants字典中，通过物理常数的名称访问该物理常数，如：

C.physical_constants['speed of light in vacuum']

(299792458.0, 'm s^-1', 0.0)

C.physical_constants['Planck constant']

(6.62606957e-34, 'J s', 2.9e-41)

C.physical_constants['electron mass']

(9.10938291e-31, 'kg', 4e-38)

返回一个包含三个值的元组，分别表示常数值、单位、误差；

scipy的special模块包含基本的数学函数、特殊数学函数、以及numpy中的所有函数；

由于浮点数的精度限制，有些函数的无法精确地表示结果，如log(1+1e-20)，1+1e-20非常接近1，得到的结果将是0，而不是精确的值；log1p(1e-20)则可以得到精确的值：

import math

import scipy.special as S

math.log(1+1e-20,10)

0.0

S.log1p(1e-20)

9.9999999999999995e-21

同时，查看文档可以了解到：log1p是一个ufunc；

2. 优化：optimize

scipy的optimize模块提供了许多数值优化算法；

1. 最小二乘拟合

optimize.leastsq()对数据进行最小二乘拟合计算。leastsq()使用时，需要传递计算误差的函数和待确定的参数的初始值p即可；

直线拟合：

def residuals(p):
    k, b = p
    return Y - (k*X - b)

X 、 Y 为两个一维数组，表示点的X轴和Y轴位置；

r = leastsq(residuals, [1,0])

leastsq()函数传入误差计算函数和初始值[1,0]，该初始值将作为误差计算函数的第一个参数传入；

计算的结果r是一个包含两个元素的元组，第一个元素是一个数组，表示拟合后的参数k、b；第二个元素如果等于1、2、3、4中的其中一个整数，则拟合成功，否则将会返回mesg ；更多的返回值见文档；

其他函数拟合（以正弦波拟合为例）：

def func(x,p):
    A,k,theta = p
    return A*np.sin(2*np.pi*k*x+theta)

def residuals(p,y,x):
    return y - func(x,p)

x = np.linspace(0,2*np.pi,100)
A, k, theta = 10, 0.34, np.pi/6   #真实参数
y0 = func(x,[A,k,theta])   #真实值
y1 = y0 + 2 * np.random.randn(len(x))  # 加入噪声
p0 = [10, 0.3, 0.5]  #猜测拟合参数，即初始值

plsq = leastsq(residuals, p0, args=(y1,x)) # 除了初始值之外，还调用了args参数，用于指定residuals中使用到的其他参数（直线拟合时直接使用了X,Y的全局变量）,同样也返回一个元组，第一个元素为拟合后的参数数组；

import  pylab as pl
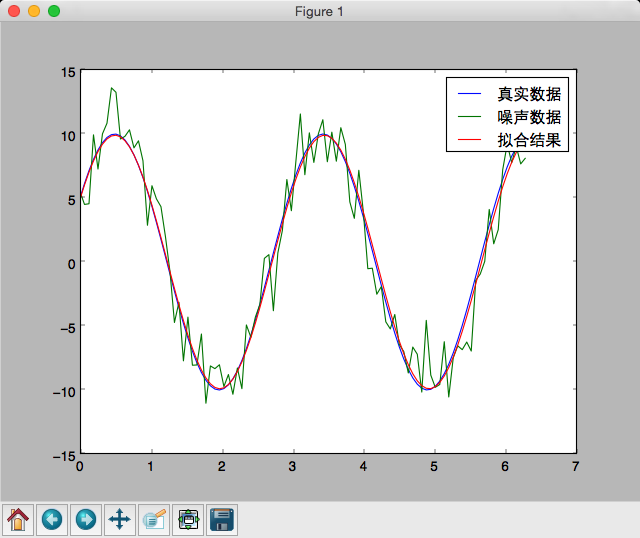
pl.plot(x,y0,label=u'真实数据')
pl.plot(x,y1,label=u'噪声数据')
pl.plot(x,func(x,plsq[0]),label=u'拟合结果')
pl.legend()
pl.show()

拟合的过程中，猜测的初始值非常重要，需要先将噪声数据画出来，然后大致估计相位和频率，推出估计的初始值，再进行拟合；

2. 函数的最小值

optimize模块还提供了许多求函数最小值的算法：fmin、fmin_powell、fmin_cg、fmin_bfgs等，这些函数通过传入目标函数和初始值对最小值进行拟合，fmin*()这个类型的函数还提供一个fprime的参数，该参数为计算目标函数对各个自变量偏导数的函数。

3. 非线性方程组的求解

optimize模块中的fsolve()函数可以求解非线性方程组，该函数传入一个计算方程组误差的函数，和参数的初始值如：

def func(x):
    u1,u2,u3 = x
    return [f1(u1,u2,u3),f2(u1,u2,u3),f3(u1,u2,u3)]

result = fsolve(func,[1,1,1])

以上过程可以求：

f1(u1,u2,u3) = 0
f2(u1,u2,u3) = 0
f3(u1,u2,u3) = 0

的非线性方程组的解；