gamma函数及相关其分布

gamma函数的定义及重要性质

\[\Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}dt\]

\[\Gamma(x+1) = x \Gamma(x)\]

\[\Gamma(n) = (n-1)! \]

\[\Gamma(0) = 1\]

\[\Gamma({1\over 2}) = 2\int_0^{+\infty}e^{-u^2}du = \sqrt\pi\]

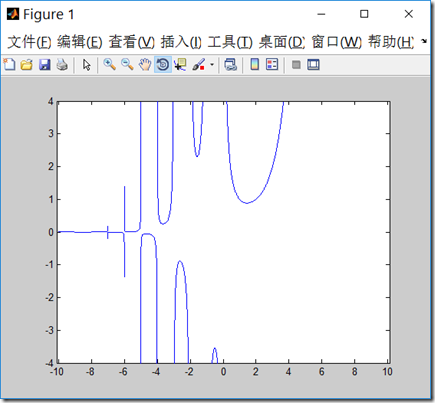
gamma函数的图像

在matlib中，我们可以方便的用下面的代码画出gamma函数的图像。

x = -10:0.001:10;

plot(x,gamma(x));

axis([-10.1,10.1,-4,4]);

随机变量\(Y=X^2\)的概率密度

假设随机变量\(X\)具有概率密度\(f_X(x),-\infty<x<\infty\),求\(Y=X^2\)的概率密度。

\begin{align*}F_Y(y) &=P(Y\leq y)=P(X^2 \leq y) \\
&=P(-\sqrt{y} \leq x \leq \sqrt{y}) \\ &=F_X(\sqrt{y})-F_X{(-\sqrt{y})} \end{align*}

\[f_Y(y)=\left\{

\begin{aligned}

\frac{1}{2\sqrt{y}}[f_X(\sqrt{y})+f_X(\sqrt{-y}], y >0, \\
0, y \leq 0 \\

\end{aligned}

\right.\]

设\(X \sim N(0,1)\)，其概率密度为\(\varphi(x)=\frac{1}{\sqrt{2\pi}}e^{\frac{-x^2}{2}}, -\infty<x<\infty\),则\(Y=X^2\)的概率密度如下：

\[f_Y(y)=\left\{
\begin{aligned}
\frac{1}{\sqrt{2\pi}}y^{-1/2}e^{-y/2}, y>0, \\
0, y \leq 0 \\
\end{aligned}
\right.\]

Gamma分布

\(X \sim \Gamma(\alpha, \theta)\)

\[f_X(x)=\left\{
\begin{aligned}
\frac{1}{\theta^\alpha\Gamma(\alpha)}x^{\alpha-1}e^{-x/\theta}, x> 0, \alpha>0,\theta>0 \\
0, x \leq 0, \alpha>0,\theta>0 \\
\end{aligned}
\right.\]

当\(\alpha= 1 , \theta = \lambda 时，\Gamma(1,\lambda)\) 就是参数为\(\lambda\)的指数分布,记为\(exp (\lambda)\) ；

当\(\alpha= n/2 , \theta = 2 时，\Gamma(n/2,1/2)\)就是数理统计中常用的\(\chi^2(n)\) 分布。

数学期望(均值)、方差分别为

\[E(X) = \alpha\theta\]

\[D(x) = \alpha\theta^2\]

Gamma分布是指在地震序列的有序性、地震发生率的齐次性、计数特征具有独立增量和平稳增量情况下，可以导出地震发生\(i\)次时间的概率密度为Gamma密度函数。

gamma分布的一个重要应用就是作为共轭分布出现在很多机器学习算法中。

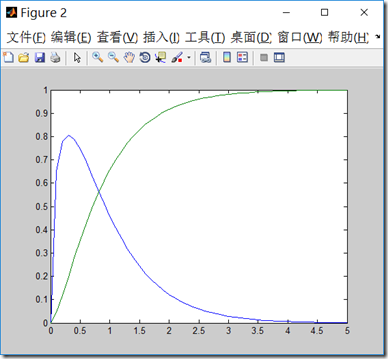
gamma的密度函数和分布函数图像如下：

注意：这儿\(\alpha=1.5,\theta = 1/0.6 或者 \beta=0.6\),因为gamma函数有两种表达方式，一种用\(\theta\),一种用\(\beta\),它们的关系是\(\theta=\frac{1}{\beta}\)

x=0:0.1:5;
figure;
plot(x,[gampdf(x,1.5,0.6);gamcdf(x,1.5,0.6)])

Gamma分布的可加性

设\(X \sim \Gamma(\alpha, \theta),Y \sim \Gamma(\beta,\theta)\),\(X,Y\)的概率密度如下：

\[f_X(x)=\left\{
\begin{aligned}
\frac{1}{\theta^\alpha\Gamma(\alpha)}x^{\alpha-1}e^{-x/\theta}, x> 0, \alpha>0,\theta>0 \\
0, x \leq 0, \alpha>0,\theta>0 \\
\end{aligned}
\right.\]

\[f_Y(y)=\left\{
\begin{aligned}
\frac{1}{\theta^\beta\Gamma(\beta)}y^{\beta-1}e^{-y/\theta}, y > 0, \beta>0,\theta>0 \\
0, y \leq 0, \beta>0,\theta>0\\
\end{aligned}
\right.\]

则有\(Z=X+Y\)的分布为：\(X+Y \sim \Gamma(\alpha + \beta,\theta)\)

\(\chi ^2\)（卡方)分布及其性质

设\(X_1,X_2,…,X_n\)是来自总体\(N(0,1)\)的样本，则称统计量

\[\chi^2=X_1^2+X_2^2+…+X_n^2\]

为服从自由度为\(n\)的\(\chi^2\)分布，记为\(\chi^2 \sim \chi^2(n)\)

它的概率密度函数为：

\[f(x,n)=\left\{
\begin{aligned}
\frac{1}{2^{n/2}\Gamma(n/2)}x^{n/2-1}e^{-x/2}, x> 0 \\
0, x \leq 0, \\
\end{aligned}
\right.\]

用下面的matlib代码，我们能够画出卡方分布概率密度函数图:

%卡方分布
x=0.0:0.01:30;
y=chi2pdf(x,1);
y1=chi2pdf(x,2);
y2=chi2pdf(x,4);
y3=chi2pdf(x,6);
y4=chi2pdf(x,11);
plot(x,y,'-r',x,y1,'-g',x,y2,'-b',x,y3,'-c',x,y4,'-m');
legend('自由度1','自由度2','自由度4','自由度6','自由度11');
axis([0,30,0,0.2]);

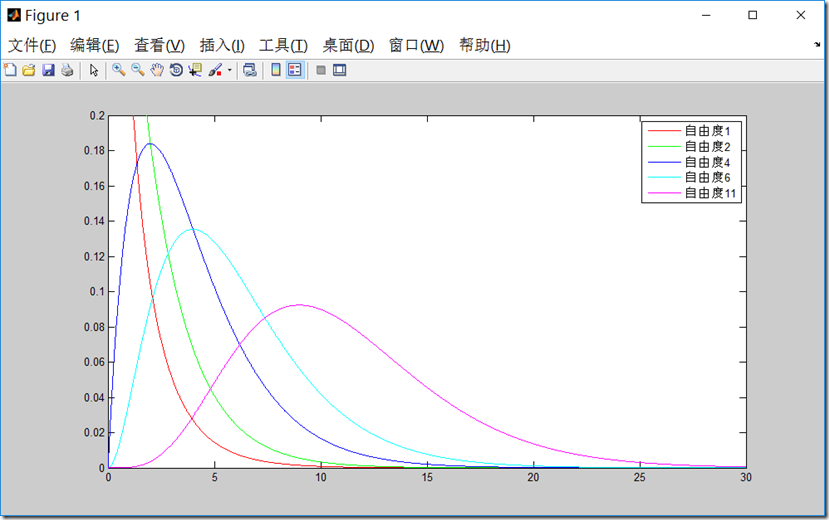
由上面的式子可以知道：

\[\chi^2=\sum\limits_{i=1}^{n}X_i^2 \sim \Gamma(\frac{n}{2},2)\]

1）若 \(X \sim \chi(n)\),则\(E(X)=n,D(X)=2n\)

2)若\(X \sim \chi(n_1)\), \(Y \sim \chi(n_2)\),且\(X,Y\)相互对立，则有\(X+Y \sim \chi^2(n_1+n_2)\)