NOIp 2018 提高组

T1铺设道路

题目描述

春春是一名道路工程师，负责铺设一条长度为 $ n $ 的道路。

铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 $ n $ 块首尾相连的区域，一开始，第 ii 块区域下陷的深度为 $ d[i] $ 。

春春每天可以选择一段连续区间 $ [L,R] $ ，填充这段区间中的每块区域，让其下陷深度减少 $ 1 $ 。在选择区间时，需要保证，区间内的每块区域在填充前下陷深度均不为 $ 0 $ 。

春春希望你能帮他设计一种方案，可以在最短的时间内将整段道路的下陷深度都变为 $ 0 $ 。

输入输出格式

输入格式：

输入文件包含两行，第一行包含一个整数 $ n $ ，表示道路的长度。第二行包含 $ n $ 个整数，相邻两数间用一个空格隔开，第 $ i $ 个整数为 $ d[i]$ 。

输出格式：

输出文件仅包含一个整数，即最少需要多少天才能完成任务。

输入输出样例

输入样例

6

4 3 2 5 3 5

输出样例

9

说明

【样例解释】

一种可行的最佳方案是，依次选择： $ [1,6] $ , $ [1,6] $ , $ [1,2] $ , $[1,1] $ , $ [4,6] $ , $ [4,4] $ , $ [4,4] $ , $ [6,6] $ , $ [6,6] $ 。

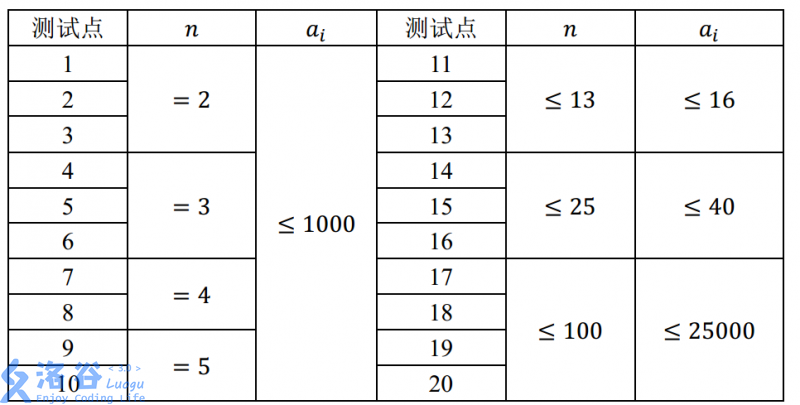
【数据规模与约定】

对于 $ %30 $ 的数据， $ 1 ≤ n ≤ 10 $ ；

对于 $ %70 $ 的数据， $ 1 ≤ n ≤ 1000 $ ；

对于 $ %100 $ 的数据，$ 1 ≤ n ≤ 100000 $ , $ 0 ≤ d[i]≤ 10000 $

分析：

整体想法是用一个 $ while $ 循环来控制指针，找出每一段不上升的子序列，将这些子序列中的第一个数加起来，因为这个数是这一段子序列中最大值，所以这个数就是这一整个序列铺设道路所用的最少时间，然后加起来就好了。

还有我觉得开始处理或者是不处理出一个最小值都没有关系。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#include <queue>
#include <map>
#include <cmath>
#define re register
using namespace std ;
const int maxn = 100005 ;
inline int read() {
	int f = 1 , x = 0 ;
	char ch = getchar() ;
	while(ch < '0' || ch > '9') {if(ch == '-') f = -1 ; ch = getchar() ;}
	while(ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + ch - '0' ;ch = getchar() ;}
	return x * f ;
}
int n , h[maxn] ;
int tmp , ans , minn = 1e9 ; 
int main() {
	n = read() ;
	for(re int i = 1 ; i <= n ; ++i) {
		h[i] = read() ;
		minn = min(minn , h[i]) ;
	}
	ans += minn ;
	for(re int i = 1 ; i <= n ; ++i)  h[i] -= minn ;
	int j = 1 ;
	while(h[j] == 0) j++ ;
	int wh = 0 , m = 1e9 ;
	while(j <= n) {
		m = h[j] ;
		ans += (h[j] - h[wh]) ;
		for(int i = j ; i <= n ; ++i) {
			if(h[i] <= m) {
				m = h[i] ;
				wh = i ;
			}
			else  break;
		}
		j = wh + 1;
	}
	printf("%d\n" , ans) ;
	return 0 ;
}

T2货币系统

题目描述

在网友的国度中共有 $ n $ 种不同面额的货币，第 $ i $ 种货币的面额为 $ a[i] $ ，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 $ n $ 、面额数组为 $ a[1..n] $ 的货币系统记作 $ (n,a) $ 。

在一个完善的货币系统中，每一个非负整数的金额 $ x $ 都应该可以被表示出，即对每一个非负整数 $ x $ ，都存在 $ n $ 个非负整数 $ t[i] $ 满足 $ a[i] \times t[i] $ 的和为 $ x $ 。然而，在网友的国度中，货币系统可能是不完善的，即可能存在金额 $ x $ 不能被该货币系统表示出。例如在货币系统 $ n=3, a=[2,5,9] $ 中，金额 $ 1,3 $ 就无法被表示出来。

两个货币系统 $ (n,a) $ 和 $ (m,b) $ 是等价的，当且仅当对于任意非负整数 $ x $ ，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 $ (m,b) $ ，满足 $ (m,b) $ 与原来的货币系统 $ (n,a) $ 等价，且 $ m $ 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 $ m $ 。

输入输出格式

输入格式：

输入文件的第一行包含一个整数 $ T $ ，表示数据的组数。

接下来按照如下格式分别给出 $ T $ 组数据。每组数据的第一行包含一个正整数 $ n $ 。接下来一行包含 $ n $ 个由空格隔开的正整数 $ a[i] $

输出格式：

输出文件共有 $ T $ 行，对于每组数据，输出一行一个正整数，表示所有与 $ (n,a) $ 等价的货币系统 $ (m,b) $ 中，最小的 $ m $ 。

输入输出样例

输入样例:

2

4

3 19 10 6

5

11 29 13 19 17

输出样例：

2

5

说明

在第一组数据中，货币系统 $ (2, [3,10]) $ 和给出的货币系统 $ (n, a) $ 等价，并可以验证不存在 $ m < 2 $ 的等价的货币系统，因此答案为 $ 2 $ 。在第二组数据中，可以验证不存在 $ m<n $ 的等价的货币系统，因此答案为 $ 5 $ 。

分析：

首先相同的数字肯定是没有意义的，我们对原数组进行去重，然后我们用一个数组 $ vis[i] $ 表示数字 $ i $ 是否能够表示，如果 $ vis[i]=true $ 可以表示，否则不可以表示。那么我们就对于 $ n $ 个数中的每一个数字进行判断，第一个 $ a[0] $ 肯定不能表示，那么我们结果 $ ans++ $ ，然后把 $ a[0] $ 能够表示的数字 $ i $ 全标记为 $ vis[i]=true $ ；那么在检查第 $ i $ 个数字，如果能够用已经标记的数字表示，那么说明这个数可以用之前的数表示，答案不记录；否则答案记录，而且将已经能够表示的数字加上 $ a[i] $ ，也进行标记 $ vis[j+a[i]]=true $ ，直至循环完毕，输出 $ ans $ 即可。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#include <queue>
#include <map>
#include <vector>
#include <cmath>
#define re register
using namespace std ;
const int maxn = 105 ;
const int Maxn = 25005 ;
inline int read() {
	char ch = getchar() ;
	int f = 1 , x = 0 ;
	while(ch > '9' || ch < '0') {if(ch == '-') f = -1 ; ch = getchar() ;}
	while(ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + ch - '0' ; ch = getchar() ;}
	return x * f ;
}
int T , n , a[maxn];
int f[maxn] , ans;
bool vis[Maxn] ;
int main() {
	T = read() ;
	while(T--) {
		n = read() ;
		memset(a , 0 , sizeof(a)) ;
		for(re int i = 1 ; i <= n ; ++i) {
			a[i] = read() ;
		}
		sort(a + 1 , a + 1 + n) ;
		n = unique(a + 1 , a + 1 + n) - a - 1;
		memset(vis , false , sizeof(vis)) ;
		vis[0] = true ;
		ans = 0 ;
		for(re int i = 1 ; i <= n ; ++i) {
			if(!vis[a[i]]) {
				ans ++ ;
				for(re int j = 0 ; j < Maxn ; ++j)
					if(j + a[i] < Maxn && vis[j])
						vis[j + a[i]] = true ;
			}
		}
		printf("%d\n" , ans) ;
	}
	return 0 ;
}