noip模拟赛 运

【问题背景】
zhx 和妹子们玩数数游戏。
【问题描述】
仅包含 4 或 7 的数被称为幸运数。
一个序列的子序列被定义为从序列中删去若干个数， 剩下的数组成的新序列。
两个子序列被定义为不同的当且仅当其中的元素在原始序列中的下标的集合不
相等。对于一个长度为 N的序列，共有 2^N个不同的子序列。（包含一个空序列）。
一个子序列被称为不幸运的， 当且仅当其中不包含两个相同的幸运数。
对于一个给定序列， 求其中长度恰好为 K 的不幸运子序列的个数， 答案 mod
10^9+7 输出。
【输入格式】
第一行两个正整数 N， K， 表示原始序列的长度和题目中的 K。
接下来一行 N 个整数 ai， 表示序列中第 i 个元素的值。
【输出格式】
仅一个数，表示不幸运子序列的个数。（mod 10^9+7）
【样例输入】
3 2
1 1 1
【样例输出】
3
【样例输入】
4 2
4 7 4 7
【样例输出】
4

【样例解释】
对于样例 1， 每个长度为 2 的子序列都是符合条件的。
对于样例 2，4个不幸运子序列元素下标分别为：{1, 2}, {3, 4}, {1, 4}, {2, 3}。
注意下标集{1, 3}对应的子序列不是“不幸运”的， 因为它包含两个相同的幸运数
4.
【数据规模与约定】

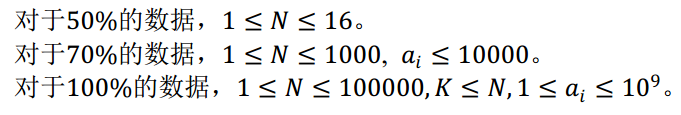
分析：好题啊！暴力做法很简单，满分做法需要具备一定的数学知识.

不幸运的数随便怎么选都行，关键是幸运的数要怎么选.可以把幸运的数提出来，用数组b保存。要选总长度为K的子序列，我们可以在b中选K1个，在不幸的数中选K2个.b中的数因为每个数只能选一个，所以可以先去重，并用一个数组cnt[i]记录第i个幸运数有多少个.注意到b中的每类数要么不选，要么就有cnt[i]种选法，一共要选K1个，很像dp,究竟能否dp呢？理论上来说是可以的，但是如果幸运数很多的话状态就表示不了.好在题目中说了ai<=10^9,大约有1000个幸运数,是完全可以dp的.

设f[i][j]表示前i类幸运数中组成长度为j的序列的方案数有多少种.b中的每类数要么不选，要么就有cnt[i]种选法，所以f[i][j] = f[i-1][j] + f[i-1][j-1] * cnt[i].K1的部分计算完了.

K2部分其实就是求若干个组合数.因为N特别大，不能用递推来求出所有的组合数，只能在需要的时候求.涉及到除法取模，所以要求逆元，又因为有很多组合数要求，所以先预处理出1到n的阶乘、逆元、逆元的阶乘就好了，最后枚举K1,K1部分的答案与K2部分的答案乘一下就可以了.

注意：K1枚举的时候K2一定不能大于不幸运数的个数.

把不同类别的东西分开处理是这道题的关键点.有很多限制的计数子问题一般都用dp,限制不多的dp和数学方法都行.

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const int mod = 1e9 + ;

ll n, a[], k, ans,m, jie[], niyuan[], nijie[], b[], cnt[], tot, tott, f[][];

void init()
{
    jie[] = ;
    jie[] = ;
    niyuan[] = ;
    nijie[] = ;
    nijie[] = ; //
    for (ll i = ; i <= n; i++)
    {
        jie[i] = (jie[i - ] * i) % mod;
        niyuan[i] = (mod - mod / i) * niyuan[mod % i] % mod;
        nijie[i] = (nijie[i - ] * niyuan[i]) % mod;
        //printf("%lld %lld %lld %lld\n", i, jie[i], niyuan[i], nijie[i]);
    }
}

bool check(ll x)
{
    while (x)
    {
        if (x %  !=  && x %  != )
            return false;
        x /= ;
    }
    return true;
}

void print()
{
    for (int i = ; i <= tott; i++)
        for (int j = ; j <= tott; j++)
            printf("%d %d %lld\n", i, j, f[i][j]);
}

int main()
{
    scanf("%lld%lld", &n, &k);
    init();
    for (ll i = ; i <= n; i++)
        scanf("%lld", &a[i]);
    for (ll i = ; i <= n; i++)
        if (check(a[i]))
            b[++tot] = a[i];
    sort(b + , b +  + tot);
    for (int i = ; i <= tot; i++)
    {
        if (b[i] != b[i - ])
            cnt[++tott] = ;
        else
            cnt[tott]++;
    }
    f[][] = ;
    for (int i = ; i <= tott; i++)
    {
        f[i][] = ;
        for (int j = ; j <= tott; j++)
            f[i][j] = (f[i - ][j] + f[i - ][j - ] * cnt[i] % mod) % mod;
    }
    //print();
    m = n - tot;
    //printf("flag! %lld\n", tott);
    for (int i = tott; i >= ; i--)
    {
        if (k - i > m)
            break;
        ll temp = jie[m] * nijie[k - i] % mod * nijie[m - k + i] % mod;
        //printf("%lld %lld %lld %lld\n", temp,m,k-i,m - k + i);
        ans = (ans + temp * f[tott][i] % mod) % mod;
    }
    printf("%lld\n", ans);

    return ;
}