OpenCASCADE Curve Length Calculation

OpenCASCADE Curve Length Calculation

eryar@163.com

Abstract. The natural parametric equations of a curve are parametric equations that represent the curve in terms of a coordinate-independent parameter, generally arc length s, instead of an arbitray variable like t or u. According to the natural equations, the curve length is the integration of the curve parametric equation’s derivation. So the core algorithm for curve length calculation is the numerical integration method. OpenCASCADE use Gauss-Legendre to calculate the integration for single variable and multiple variables. Because of curve in OpenCASCADE is single variable function, so can use the Gauss-Legendre to calculate the arc length for the curve.

Key Words. OpenCASCADE, The Gauss-Legendre Integration, Parametric Curve,

The Natural Parametric Equations,  Arc Length,

1. Introduction

对于同一条曲线，选择的参数不同其表达形式也不尽相同。而曲线自身的弧长是曲线本身的不变量，它与坐标系的选择无关，因此取曲线的弧长作为参数来研究曲线具有非常重要的意义。以曲线弧长作为曲线方程的参数，这样的方程称为曲线的自然参数方程。由曲线的自然参数方程可知曲线的弧长是曲线参数方程导数的积分。所以计算曲线弧长的核心算法成了计算函数的积分了。

OpenCASCADE中数学计算库TKMath中有一种高精度计算积分的算法Gauss-Legendre积分法，可对单变量和多变量的函数进行积分计算。由于OpenCASCADE中曲线是单变量的参数方程，所以可以用Gauss-Legendre来计算积分，进而得到曲线的弧长。如下图所示：

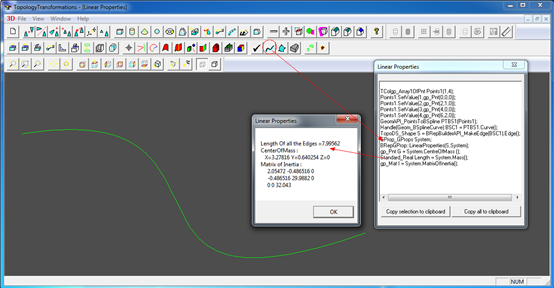
Figure 1.1 Length of Curve

本文对曲线的自然参数方程的概念进行说明，并简要介绍Gauss-Legendre算法及其在OpenCASCADE中的应用，即求曲线的弧长。

2. The Natural Parametric Equations

对于同一曲线若选择的参数不同，则其表达式亦不同，故用坐标系讨论曲线时，具有人为的性质，而曲线自身的弧长则曲线的不变量，它与坐标系的选取无关。因此，我们取曲线自身的弧长作为参数来研究曲线的内在性质。无论是理论探索还是实用研究，弧长参数化都有很重要的意义。

给定空间曲线r，在其上任取一点P0(x0, y0, z0)作为计算弧长的起点。应用弧长积分公式，即可计算该曲线上任意点P(x,y,z)到P0之间的弧长。由此，曲线上点的位置与该点处的弧长是一一对应的，如下图所示：

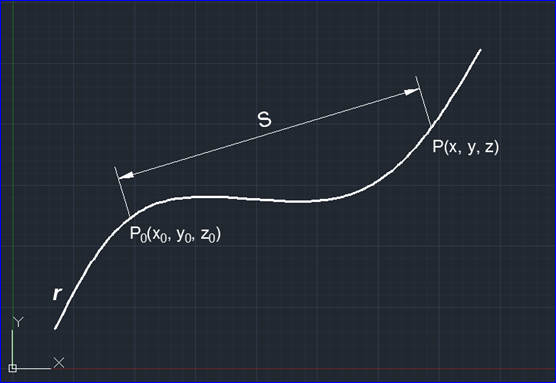
Figure 2.1 Arc length parameterization

即曲线上点的坐标是以弧长为参数的函数：

由其矢量方程可知，曲线是弧长为参数的矢函数，我们将其称为弧长参数化(Arc length parameterization)。弧长称为自然参数(Natural Parameter)，曲线方程称为自然参数方程(Natural Parametric Equations)。现讨论曲线的自然参数方程与参数方程的联系：已知曲线的矢量方程为：

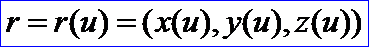
则弧长的微分和积分公式分别为：

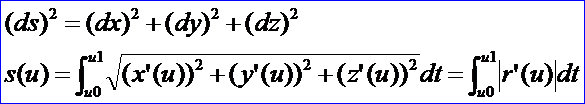
s(u)即为与参数u0和u1对应的两点P0和P之间的弧长。弧长参数化是一类重要的概念，但是如果用上式来计算弧长比较繁琐，可以通过累加弦长方法来近似计算。

给定曲线：

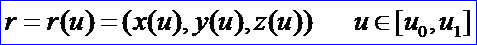
令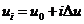是参数轴上的一个等距分划；又令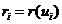为曲线上与参数ui对应的点列，则可用下式计算弦长：

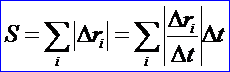
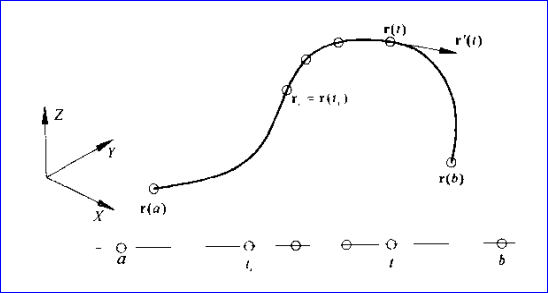
Figure 2.2 Parametric Curve

其中将参数轴等分越多，则求得的曲线的弧长越准确。

3. The Gauss-Legendre Integration

上述累加弦长的计算方法应该是Newton-Cotes积分计算法，Newton-Cotes就是将积分区间等分，并取分点为求积节点。容易看出当积分区间较大时，直接使用Newton-Cotes公式所得积分近似值的精度是很难保证的。

关于积分的数值算法有很多，其中Gauss-Legendre求积公式具有计算工作量小，所得近似值精确度高等优点，是一种高精度的求积公式。形式如下所示的求积公式：

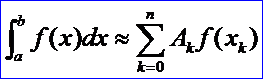
代数精度达到了2n+1，则称它为高斯型求积公式，并称相应的求积节点x0, x1, ... xn为高斯点(Gauss Point)。Ak为求积系数。

OpenCASCADE的核心模块的数学库TKMath中有Gauss-Legendre求积算法，可用来对单变量和多变量的函数进行积分计算，对应的类分别为：math_GaussSingleIntegration和math_GaussMultipleIntegration。计算所需的高斯点及系数通过查表的方式取得，数据以数组的形式在文件math.cxx中列举出，如下图所示：

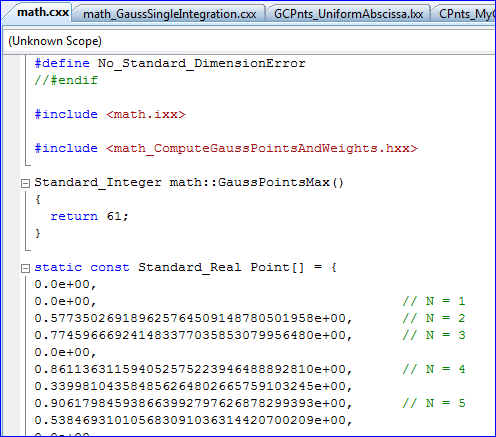
Figure 3.1 Gauss Point for Gauss-Legendre Integration

Gauss-Legendre积分用处之一就是根据曲线的自然参数方程计算曲线的弧长，代码实现如下所示：

//=====================================================================
//function : Length
//purpose  : 3d with parameters
//=====================================================================

Standard_Real CPnts_AbscissaPoint::Length(const Adaptor3d_Curve& C,
                      const Standard_Real U1,
                      const Standard_Real U2)
{
  CPnts_MyGaussFunction FG;
//POP pout WNT
  CPnts_RealFunction rf = f3d;
  FG.Init(rf,(Standard_Address)&C);
//  FG.Init(f3d,(Standard_Address)&C);
  math_GaussSingleIntegration TheLength(FG, U1, U2, order(C));
  if (!TheLength.IsDone()) {
    Standard_ConstructionError::Raise();
  }
  return Abs(TheLength.Value());
}

根据上述求曲线弧长的代码可知，只需要给定曲线及其求积区间，即可计算出此区间内曲线的弧长。因为采用直接求积计算，所得曲线的弧长值的精度还是很高的。

高斯型求积公式是一种高精度的求积公式。在求积节点数相同，即计算工作量相近的情况下，利用高斯型求积公式往往可以获得准确程序较高的积分近似值。但是，它必须在不等距的节点上计算被积函数的值，而且当节点数改变时，所用数据都要重新查表计算。

4. Conclusion

曲线自身的弧长是曲线本身的不变量，它与坐标系的选择无关，因此取曲线的弧长作为参数来研究曲线具有非常重要的意义。以曲线弧长作为曲线方程的参数，这样的方程称为曲线的自然参数方程。由曲线的自然参数方程可知曲线的弧长是曲线参数方程导数的积分。所以计算曲线弧长的核心算法成了计算函数的积分了。

在《计算方法》、《数值分析》等教材中都有关于求积分的算法，在OpenCASCADE中实现了Gauss-Legendre求积算法。Gauss-Legendre求积算法是一种高精度的求积方法。所以根据曲线的自然参数方程可知曲线弧长就是对曲线参数方程导数的求积分。所以使用高斯求积法可以得到曲线弧长较精确值。

对数值积分的具体算法感兴趣的朋友，可以参考《计算方法》、《数值分析》、《数值计算》等相关书籍。

5. References

1. 朱心雄. 自由曲线曲面造型技术. 科学出版社. 2008

2. 王仁宏, 李崇君, 朱春钢. 计算几何教程. 科学出版社. 2008

3. 易大义, 沈云宝, 李有法. 计算方法. 浙江大学出版社. 2002

4. 易大义, 陈道琦. 数值分析引论. 浙江大学出版社. 1998

5. http://mathworld.wolfram.com/NaturalParametricEquations.html

6. http://mathworld.wolfram.com/Legendre-GaussQuadrature.html

7. http://en.wikipedia.org/wiki/Gaussian_quadrature

8. http://pomax.github.io/bezierinfo/legendre-gauss.html

PDF Version: OpenCASCADE Curve Length Calculation