Jenkins系列之-—04 配置用户和权限控制

一、安装插件

插件名称：Role-based Authorization Strategy

Role Strategy Plugin插件可以对构建的项目进行授权管理，让不同的用户管理不同的项目。

二、安全配置——授权策略配置

系统管理—>全局安全配置（Configure Global Security ）,其中共有五种授权策略

1. Role-Based Strategy

1.1. 选择授权策略中的Role-Based Strategy，并点击保存

1.2. 选择系统管理—>Manage and Assign Roles （管理和分配角色）

在新开的页面中有如下3个菜单：

Manage Roles
Assign Roles
Role Strategy Macros

1.3. 选择"Manage Roles"进行角色配置。

【Global roles】全局角色配置：
添加wts这个角色并进行授权

【Project roles】项目角色配置：

添加了三个项目角色：uat，dev和test。dev用于管理开发环境的项目，test用于管理测试环境的项目。

Pattern：对构建的项目名称进行匹配，可以使用正则表达式。

【Slave roles】从属角色配置：

1.4.选择Assign Roles，分配角色

在全局角色中添加普通用户，并将普通用户加入到全局角色wts中，保证它们可以正常登录jenkins。

在项目角色中添加普通用户，并根据实际需求勾选项目角色，这样不同的用户可以对不同项目有管理权限。

2. 任何用户可以做任何事(没有任何限制)

项目内不推荐用

3. 登录用户可以做任何事

可勾选项---Allow anonymous read access（允许匿名读取访问）

4. 遗留模式

适用于Jenkins1.164以前的版本.也就是说,如果你是"admin"角色,那么你将拥有Jenkins的一切控制权,其它角色(包括匿名用户) 只有查看权限.

5. 安全矩阵

选择安全矩阵 (在配置页面将鼠标放到对应权限上即可查看帮助)：

其中有一些比较特别的权限：

Overall 的Administer 【最大权限】，拥有该权限可以干任何事情。

Overall的Read【最基本的权限】，用户必须赋予阅读的权限，不然什么都看不到。

注：

每个用户后都有2个图标，第一个是全选功能，第二个是清空功能

6. 项目矩阵授权策略

说明：安全矩阵和项目矩阵授权策略的配置是一样的，唯一的区别是项目矩阵授权策略支持在Job的配置页面再次配置授权策略。

三、踩到的坑

问题描述

首次配置jenkins的安全策略时，选择安全矩阵，但是没有给任何用户付权限，点击保存后。管理员登录失效。重新登录系统提示admin没有Overall/Read权限的异常。

解决方案：修改jenkins的config.xml配置文件。

3.1. 通过查看jenkins进程查看JENKINS_HOME的目录

ps -ef | grep jenkins

3.2. 编辑jenkins的config.xml这个配置

命令：vi /var/lib/jenkins/config.xml

配置文件如图：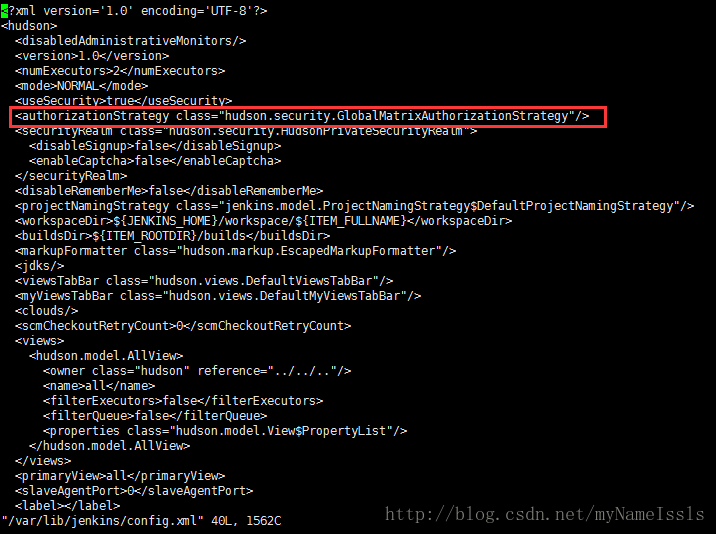

需要修改的是红线圈起来的部分。
在该标签内加入以下配置即可。

<permission>hudson.model.Hudson.Administer:anonymous</permission>

<permission>hudson.model.Hudson.ConfigureUpdateCenter:anonymous</permission>

<permission>hudson.model.Hudson.Read:anonymous</permission>

<permission>hudson.model.Hudson.RunScripts:anonymous</permission>

<permission>hudson.model.Hudson.UploadPlugins:anonymous</permission>

修改后的配置文件，如下图：

3.3 重启jenkins服务即可。