HDU Shell Necklace CDQ分治+FFT

Shell Necklace

Problem Description

Perhaps the sea‘s definition of a shell is the pearl. However, in my view, a shell necklace with n beautiful shells contains the most sincere feeling for my best lover Arrietty, but even that is not enough.

Suppose the shell necklace is a sequence of shells (not a chain end to end). Considering i continuous shells in the shell necklace, I know that there exist different schemes to decorate the i shells together with one declaration of love.

I want to decorate all the shells with some declarations of love and decorate each shell just one time. As a problem, I want to know the total number of schemes.

 

Input

There are multiple test cases(no more than 20 cases and no more than 1 in extreme case), ended by 0.

For each test cases, the first line contains an integer n, meaning the number of shells in this shell necklace, where 1≤n≤105. Following line is a sequence with nnon-negative integer a1,a2,…,an, and ai≤107 meaning the number of schemes to decorate i continuous shells together with a declaration of love.

 

Output

For each test case, print one line containing the total number of schemes module 313(Three hundred and thirteen implies the march 13th, a special and purposeful day).

 

Sample Input

3
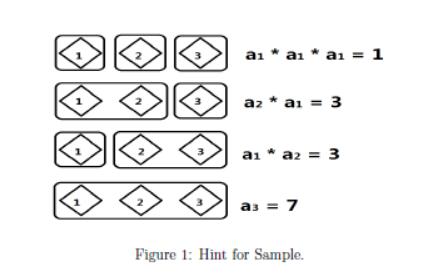
1 3 7
4
2 2 2 2
0

 

Sample Output

14
54

Hint

For the first test case in Sample Input, the Figure 1 provides all schemes about it. The total number of schemes is 1 + 3 + 3 + 7 = 14.

 

题解：

　　f[i]  = ∑ f[ n - i ] * a[i]

　　分治FFT经典题，不作赘述

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18+1LL;
const double pi = acos(-1.0);
const int N = 3e5+, M = 1e3+,inf = 2e9;

const LL mod = 313LL;

struct Complex {
    double r , i ;
    Complex () {}
    Complex ( double r , double i ) : r ( r ) , i ( i ) {}
    Complex operator + ( const Complex& t ) const {
        return Complex ( r + t.r , i + t.i ) ;
    }
    Complex operator - ( const Complex& t ) const {
        return Complex ( r - t.r , i - t.i ) ;
    }
    Complex operator * ( const Complex& t ) const {
        return Complex ( r * t.r - i * t.i , r * t.i + i * t.r ) ;
    }
} ;

void FFT ( Complex y[] , int n , int rev ) {
    for ( int i =  , j , t , k ; i < n ; ++ i ) {
        for ( j =  , t = i , k = n >>  ; k ; k >>=  , t >>=  ) j = j <<  | t &  ;
        if ( i < j ) swap ( y[i] , y[j] ) ;
    }
    for ( int s =  , ds =  ; s <= n ; ds = s , s <<=  ) {
        Complex wn = Complex ( cos ( rev *  * pi / s ) , sin ( rev *  * pi / s ) ) , w (  ,  ) , t ;
        for ( int k =  ; k < ds ; ++ k , w = w * wn ) {
            for ( int i = k ; i < n ; i += s ) {
                y[i + ds] = y[i] - ( t = w * y[i + ds] ) ;
                y[i] = y[i] + t ;
            }
        }
    }
    if ( rev == - ) for ( int i =  ; i < n ; ++ i ) y[i].r /= n ;
}
Complex y[N],s[N];

LL dp[N],a[N];
int n;
void cdq(int ll,int rr) {
     if(ll == rr) {
        dp[ll] += a[ll];
        dp[ll] %= mod;
        return ;
    }
    cdq(ll,mid);
    int len = ;
    while(len <= (rr-ll+)) len<<=;
    for(int i = ; i < len ; ++i) y[i] = Complex(,),s[i] = y[i];
    for(int i = ; i < len; ++i) y[i] = Complex(a[i+],);
    for(int i = ll; i <= mid; ++i) s[i - ll] = Complex(dp[i],);
    FFT(s,len,);FFT(y,len,);
    for(int i = ; i < len; ++i) s[i] = y[i] * s[i];
    FFT(s,len,-);
    for(int i = mid; i < rr; ++i)
        dp[i+] += LL(s[i-ll].r+0.5),dp[i] %= mod;
    cdq(mid+,rr);
}
int main() {
    while(scanf("%d",&n)!=EOF) {
        if(!n) return ;
        memset(a,,sizeof(a));
        for(int i = ; i <= n; ++i)
            scanf("%lld",&a[i]),dp[i] = ,a[i] = a[i] % mod;
        cdq(,n);
        printf("%lld\n",dp[n]);
    }
    return ;
}