Coursera Algorithms Programming Assignment 5: Kd-Trees （98分）

题目地址：http://coursera.cs.princeton.edu/algs4/assignments/kdtree.html

分析：

Brute-force implementation. 蛮力实现的方法比较简单，就是逐个遍历每个point进行比较，实现下述API就可以了，没有什么难度。

 import java.util.ArrayList;
 import java.util.TreeSet;
 import edu.princeton.cs.algs4.Point2D;
 import edu.princeton.cs.algs4.RectHV;
 import edu.princeton.cs.algs4.StdDraw;
 /**
  * @author evasean www.cnblogs.com/evasean/
  */
 public class PointSET {
     private TreeSet<Point2D> points;
     public PointSET() {
         // construct an empty set of points
         points = new TreeSet<Point2D>();
     }

     public boolean isEmpty() {
         // is the set empty?
         return points.isEmpty();
     }

     public int size() {
         // number of points in the set
         return points.size();
     }

     public void insert(Point2D p) {
         // add the point to the set (if it is not already in the set)
         if(p==null)
             throw new IllegalArgumentException("Point2D p is not illegal!");
         if(!points.contains(p))
             points.add(p);
     }

     public boolean contains(Point2D p) {
         // does the set contain point p?
         if(p==null)
             throw new IllegalArgumentException("Point2D p is not illegal!");
         return points.contains(p);
     }

     public void draw() {
         // draw all points to standard draw
         for (Point2D p : points) {
             p.draw();
         }
         StdDraw.show();
     }

     public Iterable<Point2D> range(RectHV rect) {
         // all points that are inside the rectangle (or on the boundary)
         if(rect==null)
             throw new IllegalArgumentException("RectHV rect is not illegal!");
         ArrayList<Point2D> list = new ArrayList<Point2D>();
         for(Point2D point : points){
             if(rect.contains(point)) list.add(point);
         }
         return list;
     }

     public Point2D nearest(Point2D p) {
         // a nearest neighbor in the set to point p; null if the set is empty
         if(p==null)
             throw new IllegalArgumentException("Point2D p is not illegal!");
         if(points.size() == 0) return null;
         double neareatDistance = Double.POSITIVE_INFINITY;
         Point2D nearest = null;
         for(Point2D point : points){
             double tmp = p.distanceTo(point);
             if(Double.compare(neareatDistance, tmp) == 1){
                 neareatDistance = tmp;
                 nearest = point;
             }

         }
         return nearest;
     }

     public static void main(String[] args) {
         // unit testing of the methods (optional)
     }
 }

2d-tree implementation.

kd-tree插入时要交替以x坐标和y坐标作为判断依据，比如root节点处比较依据为x坐标，那么当要查找或插入一个新节点point时，比较root节点的x坐标和point的x坐标，如果后者比前者小，那么下一次要比较的就是root->left, 相反下一次要比较的就是root->right。进入下一层级之后，就要使用y坐标作为比较依据。示例如下图：

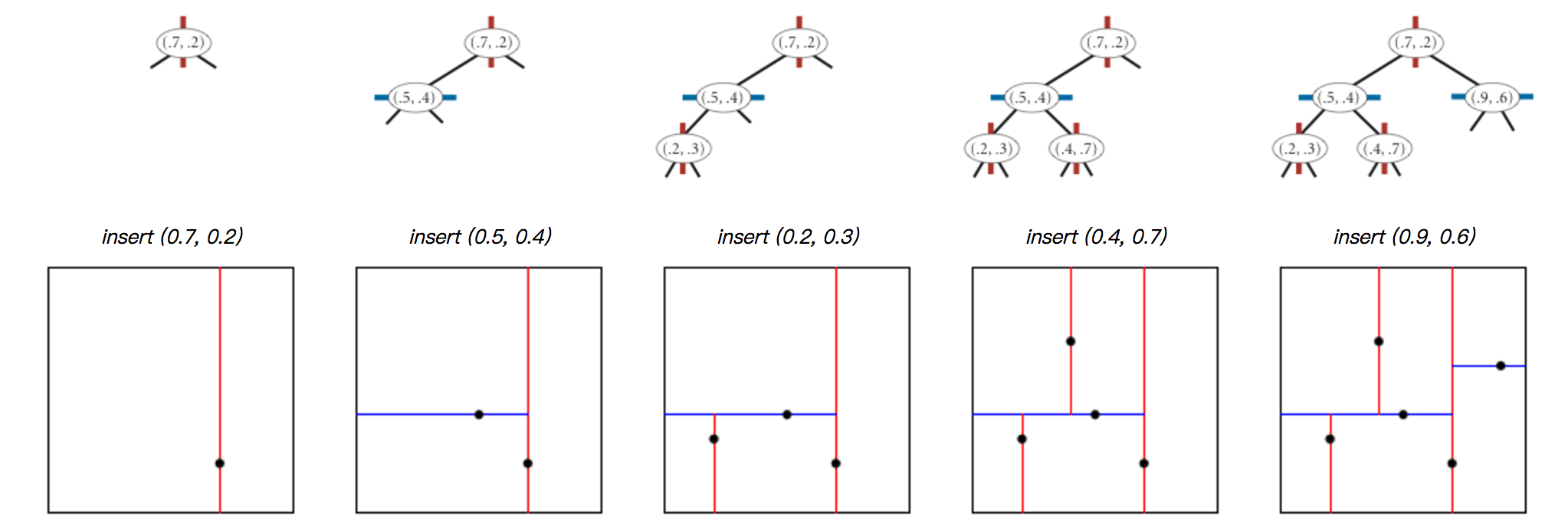
区域搜索：查找落在给定矩阵区域范围内的所有points。从root开始递归查找，如果给定的矩阵不与当前节点的相关矩阵相交，那么就没有必要继续查找该节点及其子树了。

最近节点搜索：查找与给定point距离最近的节点。从root开始递归查找其左右子树，如果给定节点point和已经查找到的最近节点的距离比该point与当前遍历节点的相关矩阵距离还近，那么就没必要遍历这个当前节点及其子树了。

 import java.util.ArrayList;
 import edu.princeton.cs.algs4.Point2D;
 import edu.princeton.cs.algs4.RectHV;
 import edu.princeton.cs.algs4.StdDraw;
 /**
  * @author evasean www.cnblogs.com/evasean/
  */
 public class KdTree {
     private Node root;
     private class Node {
         private Point2D p;
         /*
          * 节点的value就是包含该节点的矩形空间 其左右子树的矩形空间，就是通过该节点进行水平切分或垂直切分的两个子空间
          */
         private RectHV rect;
         private Node left, right;
         private int size;
         private boolean xCoordinate; // 标识该节点是否是以x坐标垂直切分

         public Node(Point2D point, RectHV rect, int size, boolean xCoordinate) {
             this.p = point;
             this.rect = rect;
             this.size = size;
             this.xCoordinate = xCoordinate;
         }
     }

     public KdTree() {
         // construct an empty set of points
     }

     public boolean isEmpty() {
         // is the set empty?
         return size() == 0;
     }

     public int size() {
         // number of points in the set
         return size(root);
     }

     private int size(Node x) {
         if (x == null)
             return 0;
         else
             return x.size;
     }

     public void insert(Point2D p) {
         // add the point to the set (if it is not already in the set)
         if (p == null)
             throw new IllegalArgumentException("Point2D p is not illegal!");
         if (root == null)
             root = new Node(p, new RectHV(0.0, 0.0, 1.0, 1.0), 1, true);
         else
             insert(root, p);
         // System.out.println("size="+root.size);
     }

     private void insert(Node x, Point2D p) {
         if (x.xCoordinate == true) { // x的切分标志是x坐标
             int cmp = Double.compare(p.x(), x.p.x());
             if (cmp == -1) {
                 if (x.left != null)
                     insert(x.left, p);
                 else {
                     RectHV parent = x.rect;
                     // 将节点x的矩形空间进行垂直切分后的左侧部分
                     double newXmin = parent.xmin();
                     double newYmin = parent.ymin();
                     double newXmax = x.p.x();
                     double newYmax = parent.ymax();
                     x.left = new Node(p, new RectHV(newXmin, newYmin, newXmax, newYmax), 1, false);
                 }
             } else if (cmp == 1) {
                 if (x.right != null)
                     insert(x.right, p);
                 else {
                     RectHV parent = x.rect;
                     // 将节点x的矩形空间进行垂直切分后的右侧部分
                     double newXmin = x.p.x();
                     double newYmin = parent.ymin();
                     double newXmax = parent.xmax();
                     double newYmax = parent.ymax();
                     x.right = new Node(p, new RectHV(newXmin, newYmin, newXmax, newYmax), 1, false);
                 }
             } else { // x.key.x() 与 p.x() 相等
                 int cmp2 = Double.compare(p.y(), x.p.y());
                 if (cmp2 == -1) {
                     if (x.left != null)
                         insert(x.left, p);
                     else {
                         x.left = new Node(p, x.rect, 1, false);
                     }
                 } else if (cmp2 == 1) {
                     if (x.right != null)
                         insert(x.right, p);
                     else {
                         x.right = new Node(p, x.rect, 1, false);
                     }
                 }
             }
         } else { // x的切分标志是y坐标
             int cmp = Double.compare(p.y(), x.p.y());
             if (cmp == -1) {
                 if (x.left != null)
                     insert(x.left, p);
                 else {
                     RectHV parent = x.rect;
                     // 将节点x的矩形空间进行垂直切分后的左侧部分
                     double newXmin = parent.xmin();
                     double newYmin = parent.ymin();
                     double newXmax = parent.xmax();
                     double newYmax = x.p.y();
                     x.left = new Node(p, new RectHV(newXmin, newYmin, newXmax, newYmax), 1, true);
                 }
             } else if (cmp == 1) {
                 if (x.right != null)
                     insert(x.right, p);
                 else {
                     RectHV parent = x.rect;
                     // 将节点x的矩形空间进行垂直切分后的左侧部分
                     double newXmin = parent.xmin();
                     double newYmin = x.p.y();
                     double newXmax = parent.xmax();
                     double newYmax = parent.ymax();
                     x.right = new Node(p, new RectHV(newXmin, newYmin, newXmax, newYmax), 1, true);
                 }
             } else { // x.key.y() 与 p.y()相等
                 int cmp2 = Double.compare(p.x(), x.p.x());
                 if (cmp2 == -1) {
                     if (x.left != null)
                         insert(x.left, p);
                     else {
                         x.left = new Node(p, x.rect, 1, true);
                     }
                 } else if (cmp2 == 1) {
                     if (x.right != null)
                         insert(x.right, p);
                     else {
                         x.right = new Node(p, x.rect, 1, true);
                     }
                 }
             }
         }
         x.size = 1 + size(x.left) + size(x.right);
     }

     public boolean contains(Point2D p) {
         // does the set contain point p?
         if (p == null)
             throw new IllegalArgumentException("Point2D p is not illegal!");
         return contains(root, p);
     }

     private boolean contains(Node x, Point2D p) {
         if(x == null ) return false;
         if (x.p.equals(p))
             return true;
         else {
             if(x.xCoordinate == true){
                 int cmp = Double.compare(p.x(), x.p.x());
                 if(cmp == -1) return contains(x.left,p);
                 else if(cmp == 1 ) return contains(x.right,p);
                 else{
                     int cmp2 = Double.compare(p.y(), x.p.y());
                     if(cmp2 == -1) return contains(x.left,p);
                     else if(cmp2 == 1 ) return contains(x.right,p);
                     else return true;
                 }
             }else{
                 int cmp = Double.compare(p.y(), x.p.y());
                 if(cmp == -1) return contains(x.left,p);
                 else if(cmp == 1 ) return contains(x.right,p);
                 else{
                     int cmp2 = Double.compare(p.x(), x.p.x());
                     if(cmp2 == -1) return contains(x.left,p);
                     else if(cmp2 == 1 ) return contains(x.right,p);
                     else return true;
                 }
             }
         }
     }

     public void draw() {
         // draw all points to standard draw
         StdDraw.setXscale(0, 1);
         StdDraw.setYscale(0, 1);
         draw(root);
     }

     private void draw(Node x) {
         if (x == null)
             return;
         StdDraw.setPenColor(StdDraw.BLACK);
         StdDraw.setPenRadius(0.01);
         x.p.draw();
         if (x.xCoordinate == true) {
             StdDraw.setPenColor(StdDraw.RED);
             StdDraw.setPenRadius();
             Point2D start = new Point2D(x.p.x(), x.rect.ymin());
             Point2D end = new Point2D(x.p.x(), x.rect.ymax());
             start.drawTo(end);
         } else {
             StdDraw.setPenColor(StdDraw.BLUE);
             StdDraw.setPenRadius();
             Point2D start = new Point2D(x.rect.xmin(), x.p.y());
             Point2D end = new Point2D(x.rect.xmax(), x.p.y());
             start.drawTo(end);
         }
         draw(x.left);
         draw(x.right);
     }

     public Iterable<Point2D> range(RectHV rect) {
         // all points that are inside the rectangle (or on the boundary)
         if (rect == null)
             throw new IllegalArgumentException("RectHV rect is not illegal!");
         if (root != null)
             return range(root, rect);
         else
             return new ArrayList<Point2D>();
     }

     private ArrayList<Point2D> range(Node x, RectHV rect) {
         ArrayList<Point2D> points = new ArrayList<Point2D>();
         if (x.rect.intersects(rect)) {
             if (rect.contains(x.p))
                 points.add(x.p);
             if (x.left != null)
                 points.addAll(range(x.left, rect));
             if (x.right != null)
                 points.addAll(range(x.right, rect));
         }
         return points;
     }

     public Point2D nearest(Point2D p) {
         // a nearest neighbor in the set to point p; null if the set is empty
         if (p == null)
             throw new IllegalArgumentException("Point2D p is not illegal!");
         if (root != null)
             return nearest(root, p, root.p);
         return null;
     }

     /**
      * 作业提交提示nearest的时间复杂度偏高，导致作业只有98分，我觉得这样写比较清晰明了，就懒得继续优化
      * @param x
      * @param p
      * @param currNearPoint
      * @return
      */
     private Point2D nearest(Node x, Point2D p, Point2D currNearPoint) {
         if(x.p.equals(p)) return x.p;
         double currMinDistance = currNearPoint.distanceTo(p);
         if (Double.compare(x.rect.distanceTo(p), currMinDistance) >= 0)
             return currNearPoint;
         else {
             double distance = x.p.distanceTo(p);
             if (Double.compare(x.p.distanceTo(p), currMinDistance) == -1) {
                 currNearPoint = x.p;
                 currMinDistance = distance;
             }
             if (x.left != null)
                 currNearPoint = nearest(x.left, p, currNearPoint);
             if (x.right != null)
                 currNearPoint = nearest(x.right, p, currNearPoint);
         }
         return currNearPoint;
     }

     public static void main(String[] args) {
         // unit testing of the methods (optional)
     }
 }