bzoj 1565 [NOI2009]植物大战僵尸【tarjan+最大权闭合子图】

一上来以为是裸的最大权闭合子图，上来就dinic

…然后没过样例。不得不说样例还是非常良心的给了一个强连通分量，要不然就WA的生活不能自理了

然后注意到有一种特殊情况：每个植物向他保护的植物连边（包括被其挡在后面的），当植物的保护范围连成一个强连通分量时，这个强连通分量上的植物以及从这个强连通分量连出去的植物，都不会在任何情况下被攻击

如下图：



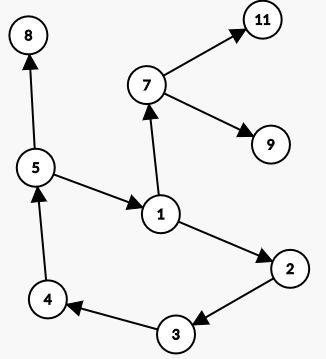
12345所形成的强连通分量不会被攻击，所以它所延伸出来的植物也不会被攻击，即图上所有点都不会被攻击

对于这种情况，用tarjan缩点，对于每个缩后的点记录一个size，对于所有 \(size[belong[u]]>1\) 的点向外dfs，记录不会被攻击到的点即可

删去所有不会被攻击到的点及其所连的边之后，跑最大权闭合子图。

具体如下：

• s点向所有正权点连边，流量为点权；所有负权点向t连边，流量为负点权（即正数！）
• 对于所有有依赖关系的点，由被保护的植物向保护植物连边（也就是把上面为tarjan建的图所有有向边反过来），也就是最大权闭合子图中的向其依赖点连边，流量为inf

\[ans=\sum 正权点点权-最小割
\]

• 割的意义：与原点相连的点表示被选择，与汇点相连的点表示不选
• S连向正权点的边被割：说明正权点被划入T侧，代表不选，收益被扣除
• 负权点连向T的边被割：说明负权点被划入S侧，代表被选，要承受惩罚
• 有依赖关系的点之间无法被割：a-->b，则如果a在S侧那b也一定在S侧

莫名跑的慢，大概是写丑了

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<vector>
using namespace std;
const int E=1000005,inf=1e9,N=55,P=1005;
int n,m,sum,h[E],cnt,le[E],s,t,v[N][N],dfn[P],tot,low[P],st[P],top,con,bl[P],si[P];
bool in[P];
vector<pair<int,int> >vec;
struct qwe
{
	int ne,to,va;
}e[E<<1];
int read()
{
	int r=0,f=1;
	char p=getchar();
	while(p>'9'||p<'0')
	{
		if(p=='-')
			f=-1;
		p=getchar();
	}
	while(p>='0'&&p<='9')
	{
		r=r*10+p-48;
		p=getchar();
	}
	return r*f;
}
void addd(int u,int v)
{//cout<<u<<" "<<v<<endl;
	vec.push_back(make_pair(u,v));
	cnt++;
	e[cnt].ne=h[u];
	e[cnt].to=v;
	h[u]=cnt;
}
void add(int u,int v,int w)
{
	cnt++;
	e[cnt].ne=h[u];
	e[cnt].to=v;
	e[cnt].va=w;
	h[u]=cnt;
}
void ins(int u,int v,int w)
{//cout<<u<<" "<<v<<" "<<w<<endl;
	add(u,v,w);
	add(v,u,0);
}
bool bfs()
{
	queue<int>q;
	memset(le,0,sizeof(le));
	le[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=h[u];i;i=e[i].ne)
			if(e[i].va>0&&!le[e[i].to])
			{
				le[e[i].to]=le[u]+1;
				q.push(e[i].to);
			}
	}
	return le[t];
}
int dfs(int u,int f)
{
	if(u==t||!f)
		return f;
	int us=0;
	for(int i=h[u];i&&us<f;i=e[i].ne)
		if(le[e[i].to]==le[u]+1&&e[i].va>0)
		{
			int t=dfs(e[i].to,min(e[i].va,f-us));
			e[i].va-=t;
			e[i^1].va+=t;
			us+=t;
		}
	if(!us)
		le[u]=0;
	return us;
}
int dinic()
{
	int re=0;
	while(bfs())
		re+=dfs(s,inf);
	return re;
}

void dfs(int u)
{
    in[u]=1;
    for(int i=h[u];i;i=e[i].ne)
        if(!in[e[i].to])
			dfs(e[i].to);
}

void tarjan(int u)
{//cout<<u<<endl;
	dfn[u]=low[u]=++tot;
	in[u]=1;
	st[++top]=u;
	for(int i=h[u];i;i=e[i].ne)
	{
		if(!dfn[e[i].to])
		{
			tarjan(e[i].to);
			low[u]=min(low[u],low[e[i].to]);
		}
		else if(in[e[i].to])
			low[u]=min(low[e[i].to],dfn[e[i].to]);
	}
	if(dfn[u]==low[u])
	{
		con++;
		while(st[top]!=u)
		{
			in[st[top]]=0;
			bl[st[top--]]=con;
			si[con]++;
		}
		in[st[top]]=0;
		bl[st[top--]]=con;
		si[con]++;
	}
}
int main()
{
	n=read(),m=read();
	t=n*m+1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			v[i][j]=read();
			int id=(i-1)*m+j,w=read(); //cout<<sor<<" "<<w<<endl;
			if(j>1)
				addd(id,id-1);
			while(w--)
			{
				int x=read()+1,y=read()+1;
				addd(id,(x-1)*m+y);
			}
		}//cout<<"ok"<<endl;
	for(int i=1;i<=n*m;i++)
		if(!dfn[i])
			tarjan(i);//,cout<<i<<endl;
	for(int i=1;i<=n*m;i++)
		if(si[bl[i]]>1&&!in[i])
			dfs(i);
	cnt=1;
	memset(h,0,sizeof(h));
	memset(e,0,sizeof(e));
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(!in[(i-1)*m+j])
			{
				int x=(i-1)*m+j;
				if(v[i][j]>=0)
					ins(s,x,v[i][j]),sum+=v[i][j];
				else
					ins(x,t,-v[i][j]);
			}
	for(int i=0;i<vec.size();i++)
		if(!in[vec[i].first]&&!in[vec[i].second])
			ins(vec[i].second,vec[i].first,inf);//cout<<"ok"<<endl;
	printf("%d\n",sum-dinic());
	return 0;
}