hdu1025 Constructing Roads In JGShining's Kingdom（二分+dp）

转载请注明出处：http://blog.csdn.net/u012860063

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1025

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.



Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource.
You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.



With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor
cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.



Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.



The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.



But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.



For example, the roads in Figure I are forbidden.








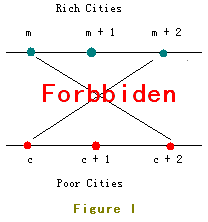
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

Input

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to
the end of file.

 

Output

For each test case, output the result in the form of sample.

You should tell JGShining what's the maximal number of road(s) can be built.

 

Sample Input

2
1 2
2 1
3
1 2
2 3
3 1

 

Sample Output

Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.

注意区分road和roads

思路：

/*如果存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7。能够看出来它的LIS长度为5。

以下一步一步试着找出它。

我们定义一个序列B，然后令 i = 1 to 9 逐个考察这个序列。

此外。我们用一个变量Len来记录如今最长算到多少了

首先。把d[1]有序地放到B里。令B[1] = 2，就是说当仅仅有1一个数字2的时候。长度为1的LIS的最小末尾是2。这时Len=1

然后，把d[2]有序地放到B里，令B[1] = 1，就是说长度为1的LIS的最小末尾是1，d[1]=2已经没用了。非常easy理解吧。

这时Len=1

接着。d[3] = 5，d[3]>B[1]。所以令B[1+1]=B[2]=d[3]=5，就是说长度为2的LIS的最小末尾是5，非常easy理解吧。这时候B[1..2]
= 1, 5，Len＝2

再来，d[4] = 3，它正好加在1,5之间。放在1的位置显然不合适。由于1小于3，长度为1的LIS最小末尾应该是1，这样非常easy推知，长度为2的LIS最小末尾是3。于是能够把5淘汰掉，这时候B[1..2]
= 1, 3，Len = 2

继续，d[5] = 6。它在3后面，由于B[2] = 3, 而6在3后面，于是非常easy能够推知B[3] = 6, 这时B[1..3]
= 1, 3, 6，还是非常easy理解吧？ Len = 3 了噢。

第6个, d[6] = 4，你看它在3和6之间，于是我们就能够把6替换掉，得到B[3] = 4。

B[1..3] = 1,
3, 4， Len继续等于3

第7个, d[7] = 8，它非常大，比4大，嗯。于是B[4] = 8。Len变成4了

第8个, d[8] = 9，得到B[5] = 9，嗯。

Len继续增大，到5了。

最后一个, d[9] = 7，它在B[3] = 4和B[4] = 8之间，所以我们知道，最新的B[4] =7。B[1..5]
= 1, 3, 4, 7, 9，Len = 5。

于是我们知道了LIS的长度为5。

!!!!! 注意。这个1,3,4,7,9不是LIS，它仅仅是存储的相应长度LIS的最小末尾。有了这个末尾，我们就能够一个一个地插入数据。尽管最后一个d[9]
= 7更新进去对于这组数据没有什么意义，可是假设后面再出现两个数字 8 和 9，那么就能够把8更新到d[5], 9更新到d[6]。得出LIS的长度为6。

然后应该发现一件事情了：在B中插入数据是有序的，并且是进行替换而不须要挪动——也就是说，我们能够使用二分查找。将每个数字的插入时间优化到O(logN)~~~~~于是算法的时间复杂度就减少到了O(NlogN)～

注意 把第一列的城市看成固定的，求出还有一列数的最长递增序列

用ans[x]保存rich city的标号y，dp[i]存放的是长度为i的序列的末尾最小的那个ans[i]值

dp[]的长度就是最多的道路数目。



设辅助数组为dp[]。

能够知道最短len=1；此时dp[1]=ans[1]。若第二个元素要大于第一个，把它增加dp[2]。len++,

否则就更新dp[1]。len不加。分析第三元素就能够推广到n个了，这样就减少分析问题的难度了。

假设第三个大于第二个元素就增加dp[3]中,假设小于第二个。直接更新dp[2]。

要推断left>len（left代表dp数组中更新元素的位置）这样2==2，不须要加。

假设小于第一个，更新dp[1],len=2>1。不须要加。

通过进一步分析：我们发现，dp数组中是递增的。它含有的元素的个数是当前上升子序列的个数（除0），

当有数据不是增加dp数组中，要更新前面的（用二分法找）.而它不会影响结果，

由于dp数组中值（除0以外）的个数并没添加，要使len 添加，有两种可能：

1:后面有元素大于dp数组的最后一个元素就有(left>len)。

2:被还有一个元素连续更新,且更新到left>len,意思就是说：选出还有一元素它能比当前元素构造的上升子序列要多。

这样就能选出最长上升子序列了。

*/

代码例如以下：

#include <cstdio>
#include <cstring>
const int maxn = 500047;
int dp[maxn], ans[maxn], n;
int LIS()
{
    dp[1] = ans[1]; //dp[i]用来存储长度为i时的最小值
    int len = 1;
    for (int i = 2; i <= n; i++)
	{
        int left = 1, right = len;
        while (left <= right)//二分查找应该更新的元素
		{
            int m = (left + right)/2;
            if (ans[i] > dp[m])
				left = m + 1;
            else
				right = m - 1;
        }
        dp[left] = ans[i];
        if (left > len)
			len = left;
    }
    return len;
}
int main()
{
    int x, y,k = 1;
    while (~scanf("%d", &n))
	{
        for (int i = 0; i < n; i++)
		{

            scanf("%d%d", &x, &y);
            ans[x] = y;
        }
        memset(dp, 0, sizeof(dp));
        int len = LIS();
        printf("Case %d:\n",k);
        if(len==1)
			printf("My king, at most 1 road can be built.");
        else
			printf("My king, at most %d roads can be built.",len);
        printf("\n\n");
        k++;
    }
    return 0;
}