[ NOIP 2009 ] TG

\(\\\)

\(\#A\) \(Spy\)

给出两个长度均为\(N\)相同的样例串，建立第一个串各个字符向第二个串对应位置字符的映射，并用映射转换给出的长度为\(M\)第三个串，输入保证只有大写字符。

若出现\(26\)个大写字符未建立完整，映射一些字符映射所得字符相同或同一个字符建立多个映射，则视为不合法，输出\(“failed”\)。否则，输出转换后的串。

\(N,M\in [1,100]\)

字符串处理题，开三个数组分别记录两个样例串每个字符是否出现，以即映射。
在建立映射时，判断已有映射与先前建立的映射是否相同、新建映射所得字符是否被作为映射答案出现过。

#include<cmath>

#include<cstdio>

#include<cctype>

#include<cstring>

#include<cstdlib>

#include<iostream>

#include<algorithm>

#define N 30

#define M 110

#define R register

using namespace std;

bool v1[N],v2[N];

int to[N],now[M],p;

int main(){

  char c=getchar();

  while(!isupper(c)) c=getchar();

  while(isupper(c)){

    now[++now[0]]=c-'A'+1;

    v1[c-'A'+1]=1; c=getchar();

  }

  for(R int i=1;i<=26;++i) if(!v1[i]){puts("Failed");return 0;}

  while(!isupper(c)) c=getchar();

  while(isupper(c)){

    int x=now[++p];

    if(to[x]){if('A'+to[x]-1!=c){puts("Failed");return 0;}}

    else if(v2[c-'A'+1]){puts("Failed");return 0;}

    else to[x]=c-'A'+1;

    v2[c-'A'+1]=1; c=getchar();

  }

  while(!isupper(c)) c=getchar();

  while(isupper(c)){

    putchar((char)'A'+to[c-'A'+1]-1);

    c=getchar();

  }

  return 0;

}

\(\\\)

\(\#B\) \(Son\)

\(N\)组数据，每组给出四个正整数\(a_0,a_1,b_0,b_1\)，求满足\(gcd(x,a_0)=a_1,lcm[x,b_0]=b_1\)的\(x\)的个数。

\(N\in [1,200]\)，\(a_0,a_1,b_0,b_1\in [1,2\times 10^9]\)

由 \(gcd(x,a_0)=a_1\) 得 \(gcd(\frac{x}{a_1},\frac{a_0}{a_1})=1\)
由 \(lcm[x,b_0]=b_1\) 得 \(gcd(x,b_0)=\frac{x\times b_0}{b_1}\)，有 \(gcd(\frac{x}{gcd(x,b_0)},\frac{b_0}{gcd(x,b_0)})=gcd(\frac{b_1}{b_0},\frac{b_1}{x})=1\)
由上知合法的\(x\)一定是\(a_1\)的倍数，一定是\(b_1\)的因数，所以得到一个做法，试除法\(\Theta(\sqrt b_1)\)求\(b_1\)因数，判断是否为\(a_1\)因数，再进一步判断推出的两个条件是否成立，总复杂度\(\Theta(N\sqrt {2\times10^9}log(2\times10^9))\approx\Theta(8\times 10^7)\)

#include<cmath>

#include<cstdio>

#include<cctype>

#include<cstring>

#include<cstdlib>

#include<iostream>

#include<algorithm>

#define R register

#define gc getchar

using namespace std;

inline int rd(){

	int x=0; char c=gc();

	while(!isdigit(c)) c=gc();

	while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}

	return x;

}

inline int gcd(int x,int y){return y?gcd(y,x%y):x;}

inline void work(){

	int a0=rd(),a1=rd(),b0=rd(),b1=rd();

  int ans=0,lim=sqrt(b1); a0/=a1; b0=b1/b0;

	for(R int x=1;x<=lim;++x)

		if(!(b1%x)){

			if(!(x%a1)&&gcd(x/a1,a0)==1&&gcd(b1/x,b0)==1)++ans;

			if(x*x==b1)continue;

			int k=b1/x;

			if(!(k%a1)&&gcd(k/a1,a0)==1&&gcd(b1/k,b0)==1)++ans;

		}

	printf("%d\n",ans);

}

int main(){

	int t=rd();

	while(t--)work();

	return 0;

}

\(\\\)

\(\#C\) \(Trade\)

给出一个\(N\)个节点\(M\)条边的图，边有向边和无向边两种，每个点有点权\(V_i\)。

求出一条从\(1\)号节点到\(N\)号节点的路径，使得在路径上有两个点\(u,v\)，保证\(u\)在\(v\)之前出现，且\(V_v-V_u\)的值最大，输出该值即可。

\(N\in [1,10^5]\)，\(M\in [1,5\times 10^5]\)，\(V_i\in [1,100]\)

最短路：

考虑无向边拆成两条有向边，跑一个以\(1\)为源的单源最短路，统计从\(1\)号节点到该节点路径上最小点权，更新变成\(dismin[v]=min(dismin[u],V_v)\)，该值代表若选择从\(1\)号节点到这个节点的路径，选这个点作为\(u\)点。
然后就是统计从这个点到\(n\)号节点路径上最大点权，代表选这个点作为\(u\)点，统计方式可以考虑建一个反图，跑以\(n\)为源的单元最短路，统计从\(n\)号节点到该节点路径上的最大点权，也就是原图中从该节点到\(n\)号节点的最大点权，更新变成\(dismax[v]=max(dismax[u],V_v)\)。
对每个点用\(dismax[i]-dismin[i]\)更新答案即可。

注意到题目所给图较稀疏，\(SPFA\)运行效率比堆优化\(Dijkstra\)实测更优秀一些。

\(SPFA\)版本

#include<cmath>

#include<queue>

#include<cstdio>

#include<cctype>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

#define N 100010

#define M 1000010

#define R register

#define gc getchar

using namespace std;

inline int rd(){

  int x=0; bool f=0; char c=gc();

  while(!isdigit(c)){if(c=='-')f=1;c=gc();}

  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}

  return f?-x:x;

}

int hd1[N],hd2[N],tot1,tot2;

struct edge{int to,nxt;}e1[M],e2[M];

inline void add1(int u,int v){

  e1[++tot1].to=v; e1[tot1].nxt=hd1[u]; hd1[u]=tot1;

}

inline void add2(int u,int v){

  e2[++tot2].to=v; e2[tot2].nxt=hd2[u]; hd2[u]=tot2;

}

bool vis1[N],vis2[N];

int n,m,ans,mn[N],mx[N],val[N];

queue<int> q1,q2;

inline void SPFA1(){

    memset(mn,0x3f,sizeof(mn));

    mn[1]=val[1]; q1.push(1);

    while(!q1.empty()){

      int u=q1.front(); q1.pop(); vis1[u]=0;

      for(R int i=hd1[u],v;i;i=e1[i].nxt)

        if(mn[v=e1[i].to]>min(val[v],mn[u])){

            mn[v]=min(val[v],mn[u]);

            if(!vis1[v]) q1.push(v); vis1[v]=1;

        }

    }

}

inline void SPFA2(){

    mx[n]=val[n]; q2.push(n);

    while(!q2.empty()){

      int u=q2.front(); q2.pop(); vis2[u]=0;

      for(R int i=hd2[u],v;i;i=e2[i].nxt)

        if(mx[v=e2[i].to]<max(val[v],mx[u])){

            mx[v]=max(val[v],mx[u]);

            if(!vis2[v]) q2.push(v); vis2[v]=1;

        }

    }

}

int main(){

  n=rd(); m=rd();

  for(R int i=1;i<=n;++i) val[i]=rd();

  for(R int i=1,u,v,w;i<=m;++i){

    u=rd(); v=rd(); w=rd();

    add1(u,v); add2(v,u);

    if(w==2){add1(v,u); add2(u,v);}

  }

  SPFA1(); SPFA2();

  for(R int i=1;i<=n;++i) ans=max(ans,mx[i]-mn[i]);

  printf("%d\n",ans);

  return 0;

}

\(Dijkstra\)版本

#include<cmath>

#include<queue>

#include<cstdio>

#include<cctype>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

#define N 100010

#define M 1000010

#define R register

#define gc getchar

using namespace std;

inline int rd(){

  int x=0; bool f=0; char c=gc();

  while(!isdigit(c)){if(c=='-')f=1;c=gc();}

  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}

  return f?-x:x;

}

int hd1[N],hd2[N],tot1,tot2;

struct edge{int to,nxt;}e1[M],e2[M];

inline void add1(int u,int v){

  e1[++tot1].to=v; e1[tot1].nxt=hd1[u]; hd1[u]=tot1;

}

inline void add2(int u,int v){

  e2[++tot2].to=v; e2[tot2].nxt=hd2[u]; hd2[u]=tot2;

}

bool vis1[N],vis2[N];

int n,m,ans,mn[N],mx[N],val[N];

priority_queue<pair<int,int> > q1,q2;

inline void dij1(){

    memset(mn,0x3f,sizeof(mn));

    mn[1]=val[1];

    q1.push(make_pair(-val[1],1));

    while(!q1.empty()){

      int u=q1.top().second; q1.pop();

      if(vis1[u]) continue; vis1[u]=1;

      for(R int i=hd1[u],v;i;i=e1[i].nxt)

        if(mn[v=e1[i].to]>min(val[v],mn[u])){

          mn[v]=min(val[v],mn[u]);

          q1.push(make_pair(-mn[v],v));

        }

    }

}

inline void dij2(){

    mx[n]=val[n];

    q2.push(make_pair(val[n],n));

    while(!q2.empty()){

      int u=q2.top().second; q2.pop();

      if(vis2[u]) continue; vis2[u]=1;

      for(R int i=hd2[u],v;i;i=e2[i].nxt)

        if(mx[v=e2[i].to]<max(val[v],mx[u])){

          mx[v]=max(val[v],mx[u]);

          q2.push(make_pair(mx[v],v));

        }

    }

}

int main(){

  n=rd(); m=rd();

  for(R int i=1;i<=n;++i) val[i]=rd();

  for(R int i=1,u,v,w;i<=m;++i){

    u=rd(); v=rd(); w=rd();

    add1(u,v); add2(v,u);

    if(w==2){add1(v,u); add2(u,v);}

  }

  dij1(); dij2();

  for(R int i=1;i<=n;++i) ans=max(ans,mx[i]-mn[i]);

  printf("%d\n",ans);

  return 0;

}

\(Tarjan+DFS\)：

同样无向边拆成两条有向边，\(Tarjan\)找\(SCC\)缩点，记录每个\(SCC\)内最大点权和最小点权，因为\(SCC\)内可以一直转圈，所以最大最小点权在这个\(SCC\)内一定可以得到。建新图时注意，若为节省空间使用同一个邻接表，需清空\(head\)数组。
考虑到缩点后一些路径不会经过\(1\)号或\(N\)号节点，所以不能拓扑排序，只能记忆化搜索。记\(f_i\)表示\(i\)号结点到\(N\)号节点的路径上的最大值。为了防止路径不可由\(1\)号节点引出，可以选择只从\(1\)号节点\(DFS\)。防止路径不可到达\(N\)号节点，选择只有到达\(N\)号节点所属\(SCC\)时才更新\(f\)数组，其余时由其他可达点更新当前点。

若\(DFS\)所有可达点之后\(f_i\)不是默认值则证明其可达\(N\)号节点，则可进一步用\(sccmax_{i}\)更新\(f_i\)，并进一步用\(f_i-sccmin_i\)更新答案，代表在这个\(SCC\)买入，在从此开始后续\(SCC\)中最大点卖出。

#include<cmath>

#include<cstdio>

#include<cctype>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

#define N 100010

#define M 500010

#define R register

#define gc getchar

#define top stk[0]

using namespace std;

bool vis[N];

int n,m,tot,ans,hd[N],val[N],f[N];

int num,cnt,low[N],dfn[N],bl[N],stk[N],mn[N],mx[N];

struct adjlist{int to,nxt;}e[M<<1];

struct Edge{int x,y;}edge[M<<1];

inline void add(int u,int v){

  e[++tot].to=v; e[tot].nxt=hd[u]; hd[u]=tot;

}

inline int rd(){

  int x=0; bool f=0; char c=gc();

  while(!isdigit(c)){if(c=='-')f=1;c=gc();}

  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}

  return f?-x:x;

}

inline void tarjan(int u){

  stk[++top]=u; vis[u]=1;

  dfn[u]=low[u]=++cnt;

  for(R int i=hd[u],v;i;i=e[i].nxt)

    if(!dfn[v=e[i].to]){

      tarjan(v); low[u]=min(low[u],low[v]);

    }

    else if(vis[v]) low[u]=min(low[u],dfn[v]);

  if(dfn[u]==low[u]){

    ++num;

    do{

      bl[stk[top]]=num;

      vis[stk[top]]=0;

      mn[num]=min(mn[num],val[stk[top]]);

      mx[num]=max(mx[num],val[stk[top--]]);

    }while(stk[top+1]!=u);

  }

}

inline bool cmp(Edge a,Edge b){return (a.x==b.x)?(a.y<b.y):a.x<b.x;}

inline void dfs(int u){

  vis[u]=1;

  if(u==bl[n]) f[u]=max(f[u],mx[u]);

  for(R int i=hd[u],v;i;i=e[i].nxt){

    if(!vis[v=e[i].to]) dfs(v);

    f[u]=max(f[u],f[v]);

  }

  if(f[u]) f[u]=max(f[u],mx[u]);

  ans=max(ans,f[u]-mn[u]);

}

int main(){

  n=rd(); m=rd();

  for(R int i=1;i<=n;++i) val[i]=rd();

  for(R int i=1,u,v;i<=m;++i){

    u=rd(); v=rd();

    add(u,v); if(rd()==2) add(v,u);

  }

  memset(mn,0x3f,sizeof(mn)); tarjan(1);

  int tmp=0; tot=0;

  for(R int i=1;i<=n;++i)

    for(R int j=hd[i],v;j;j=e[j].nxt)

      if(bl[i]!=bl[v=e[j].to]){edge[++tmp].x=bl[i];edge[tmp].y=bl[v];}

  sort(edge+1,edge+1+tmp,cmp);

  memset(hd,0,sizeof(hd));

  for(R int i=1;i<=tmp;++i)

    if(edge[i].x!=edge[i-1].x||edge[i].y!=edge[i-1].y) add(edge[i].x,edge[i].y);

  dfs(bl[1]);

  printf("%d\n",ans);

  return 0;

}

\(\\\)

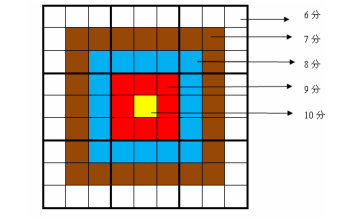
\(\#D\) \(Sudoku\)

给出一个未完成的九宫数独，并定义每一个位置的权值：

求保证填数合法的前提下，完成这个数独所能得到的权值和最大是多少。

数据保证已填入的数不少于\(24\)个。

\(DFS:\)

扫描一遍整个数独，记录下所有待填数的位置，同时记录该位置可能填入的数字，按顺序搜索到合法解即可。
一个看起来正确的优化是按照可能填入的数字个数排序，或按照所在行\(/\)列\(/\)宫剩余位置个数排序，这样在搜索的时候能够使搜索树上的较低层节点数尽可能地优秀。
实测不开\(\text O 2\)最好的状态下只会超时\(1\)个点。

#include<cmath>

#include<cstdio>

#include<cctype>

#include<cstring>

#include<cstdlib>

#include<iostream>

#include<algorithm>

#define R register

#define gc getchar

using namespace std;

inline int rd(){

  int x=0; bool f=0; char c=gc();

  while(!isdigit(c)){if(c=='-')f=1;c=gc();}

  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}

  return f?-x:x;

}

bool h[10][10],l[10][10],g[10][10];

int num[10][10],bl[10][10];

int ans=-1,numh[10],numl[10],numg[10];

int tot,val[10][10]={

{0,0,0,0,0,0,0,0,0,0},

{0,6,6,6,6,6,6,6,6,6},

{0,6,7,7,7,7,7,7,7,6},

{0,6,7,8,8,8,8,8,7,6},

{0,6,7,8,9,9,9,8,7,6},

{0,6,7,8,9,10,9,8,7,6},

{0,6,7,8,9,9,9,8,7,6},

{0,6,7,8,8,8,8,8,7,6},

{0,6,7,7,7,7,7,7,7,6},

{0,6,6,6,6,6,6,6,6,6}};

struct points{int x,y,w;}p[90];

inline void add(int x,int y){

  p[++tot].x=x; p[tot].y=y; p[tot].w=0;

  for(R int i=1;i<=9;++i){

      if(h[x][i]||l[y][i]||g[bl[x][y]][i])continue;

      else ++p[tot].w;

  }

}

inline bool cmp(points x,points y){

  if(numl[x.y]!=numl[y.y]) return numl[x.y]<numl[y.y];

  else if(numh[x.x]!=numh[y.x]) return numh[x.x]<numh[y.x];

  else if(g[bl[x.x][x.y]]!=g[bl[y.x][y.y]]) return g[bl[x.x][x.y]]<g[bl[y.x][y.y]];

  else return x.w<y.w;

}

inline int calc(){

    int res=0;

    for(R int i=1;i<=9;++i)

      for(R int j=1;j<=9;++j)

        res+=val[i][j]*num[i][j];

    return res;

}

inline void dfs(int t,int sum){

  if(t==tot+1){ans=max(ans,sum);return;}

  int x=p[t].x,y=p[t].y;

  for(R int i=1;i<=9;++i){

    if(h[x][i]||l[y][i]||g[bl[x][y]][i]) continue;

    else{

      h[x][i]=l[y][i]=g[bl[x][y]][i]=1;

      dfs(t+1,sum+i*val[x][y]);

      h[x][i]=l[y][i]=g[bl[x][y]][i]=0;

    }

  }

}

int main(){

  for(R int i=1;i<=9;++i)

      for(R int j=1;j<=9;++j){

        h[i][num[i][j]=rd()]=1;

        if(num[i][j]==0) ++numh[i];

      }

  for(R int j=1;j<=9;++j)

      for(R int i=1;i<=9;++i){

        l[j][num[i][j]]=1;

        if(num[i][j]==0) ++numl[j];

      }

  for(R int i=1;i<=7;i+=3){

    for(R int j=1;j<=3;++j)

        for(R int k=i;k<=i+2;++k){

          g[i][num[j][k]]=1;bl[j][k]=i;

          if(num[j][k]==0) ++numg[i];

        }

    for(R int j=4;j<=6;++j)

        for(R int k=i;k<=i+2;++k){

          g[i+1][num[j][k]]=1;bl[j][k]=i+1;

          if(num[j][k]==0) ++numg[i+1];

        }

    for(R int j=7;j<=9;++j)

        for(R int k=i;k<=i+2;++k){

            g[i+2][num[j][k]]=1;bl[j][k]=i+2;

            if(num[j][k]==0) ++numg[i+2];

        }

  }

  int tmp=0;

  for(R int i=1;i<=9;++i)

    for(R int j=1;j<=9;++j)

      if(!num[i][j]) add(i,j);

      else tmp+=val[i][j]*num[i][j];

  sort(p+1,p+1+tot,cmp);

  dfs(1,tmp);

  printf("%d\n",ans);

  return 0;

}

\(Dancing\ Links\ X:\)

基本的数独转精确覆盖问题及\(Dancing\ Links\ X\)解法可以参考：\(Dancing\ Links\ X\)
与基本的数独做法相同，但在找到答案之后不直接\(return\)，而要搜完所有的状态。
在计算过程中\(dance\)函数可以传一个当前权值和的参数，因为每一行只代表一个位置的一个方案，所以具体的实现过程可以对每一行先绑定权值，然后选择行的时候答案就可以直接累加了。

#include<cmath>

#include<vector>

#include<cstdio>

#include<cctype>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

#define N 750

#define M 350

#define S 247500

#define R register

#define gc getchar

using namespace std;

inline int rd(){

  int x=0; bool f=0; char c=gc();

  while(!isdigit(c)){if(c=='-')f=1;c=gc();}

  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}

  return f?-x:x;

}

inline int calc(int x,int y,int k){return x*81+y*9+k+1;}

inline void restore(int ans,int &x,int &y,int &k){

  k=(--ans)%9; ans/=9; y=ans%9; x=(ans/9)%9;

}

vector<int> res;

int t,n,m,maxr=729,maxc=324,num[10][10];

const int score[9][9]={

  {6,6,6,6,6,6,6,6,6},

  {6,7,7,7,7,7,7,7,6},

  {6,7,8,8,8,8,8,7,6},

  {6,7,8,9,9,9,8,7,6},

  {6,7,8,9,10,9,8,7,6},

  {6,7,8,9,9,9,8,7,6},

  {6,7,8,8,8,8,8,7,6},

  {6,7,7,7,7,7,7,7,6},

  {6,6,6,6,6,6,6,6,6}

};

struct dlx{

  int n,m,tot,ans=-1,s[M],h[N];

    int u[S],d[S],l[S],r[S],row[S],col[S];

  inline void reset(int _n,int _m){

    n=_n; m=_m;

    for(R int i=0;i<=m;++i){l[i]=i-1; r[i]=i+1; u[i]=d[i]=i;}

    l[0]=m; r[m]=0; tot=m;

    memset(s,0,sizeof(s));

    memset(h,-1,sizeof(h));

  }

  inline void insert(int x,int y,int k){

    row[++tot]=k; col[tot]=y; ++s[y];

    u[tot]=u[y]; d[tot]=y;

    d[u[tot]]=tot; u[d[tot]]=tot;

    if(h[x]==-1){h[x]=tot; l[tot]=tot; r[tot]=tot;}

    else{

      l[tot]=l[h[x]]; r[tot]=h[x];

      r[l[tot]]=tot; l[r[tot]]=tot;

    }

  }

  inline void remove(int y){

    r[l[y]]=r[y]; l[r[y]]=l[y];

    for(R int i=d[y];i!=y;i=d[i])

      for(R int j=r[i];j!=i;j=r[j]){

        u[d[j]]=u[j]; d[u[j]]=d[j]; --s[col[j]];

      }

  }

  inline void restore(int y){

    for(R int i=d[y];i!=y;i=d[i])

      for(R int j=r[i];j!=i;j=r[j]){

        u[d[j]]=j; d[u[j]]=j; ++s[col[j]];

      }

    r[l[y]]=y; l[r[y]]=y;

  }

  inline void dance(int sum){

    if(r[0]==0){ans=max(ans,sum);return;}

    int y=r[0];

    for(R int i=r[0];i!=0;i=r[i]) if(s[i]<s[y]) y=i;

    remove(y);

    for(R int i=d[y];i!=y;i=d[i]){

      for(R int j=r[i];j!=i;j=r[j]) remove(col[j]);

      dance(sum+row[i]);

      for(R int j=l[i];j!=i;j=l[j]) restore(col[j]);

    }

    restore(y); return;

  }

}dlx;

int main(){

  dlx.reset(maxr,maxc);

  for(R int i=0;i<=8;++i)

    for(R int j=0;j<=8;++j) num[i][j]=rd();

  for(R int i=0;i<=8;++i)

    for(R int j=0;j<=8;++j)

      for(R int k=0;k<=8;++k)

        if(num[i][j]==0||num[i][j]==k+1){

          int x=calc(i,j,k);

          dlx.insert(x,calc(0,i,j),score[i][j]*(k+1));

          dlx.insert(x,calc(1,i,k),score[i][j]*(k+1));

          dlx.insert(x,calc(2,j,k),score[i][j]*(k+1));

          dlx.insert(x,calc(3,(i/3)*3+j/3,k),score[i][j]*(k+1));

        }

  dlx.dance(0);

  printf("%d\n",dlx.ans);

  return 0;

}

[ NOIP 2009 ] TG的更多相关文章

最优贸易 NOIP 2009 提高组第三题
题目描述 C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市.任意两个城市之间最多只有一条道路直接相连.这 m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路 ...
NOIP 2009 潜伏者
P1071 潜伏者题目描述 RR 国和 SS 国正陷入战火之中,双方都互派间谍,潜入对方内部,伺机行动.历尽艰险后,潜伏于 SS 国的 RR 国间谍小 CC 终于摸清了 SS 国军用密码的编码规则: ...
洛谷P1067 多项式输出 NOIP 2009 普及组第一题
洛谷P1067 多项式输出 NOIP 2009 普及组第一题题目描述一元n次多项式可用如下的表达式表示: 输入输出格式输入格式输入共有 2 行第一行 1 个整数,n,表示一元多项式的次数. ...
NOIP 2009 靶形数独（DLX）
小城和小华都是热爱数学的好学生,最近,他们不约而同地迷上了数独游戏,好胜的他们想用数独来一比高低.但普通的数独对他们来说都过于简单了,于是他们向Z 博士请教,Z 博士拿出了他最近发明的“靶形数独”,作 ...
[ NOIP 2014 ] TG
\(\\\) \(Day\ 1\) \(\\\) \(\#\ A\) \(Rps\) 定义五种方案的石头剪刀布游戏,两人共进行\(N\)局游戏,已知两人各自的循环节和具体方案,胜者得\(1\)分,败者 ...
NOIp #2009
http://files.cnblogs.com/files/radiumlrb/NOIP2009%E6%8F%90%E9%AB%98%E7%BB%84%E5%A4%8D%E8%B5%9B%E8%AF ...
noip 2009 细胞分裂
/*数论题考察唯一分解定理当然用到一些技巧*/ #include<iostream> #include<cstdio> #include<cstring> #d ...
noip 2009 道路游戏
/*10分钟的暴力意料之中的5分..*/ #include<iostream> #include<cstdio> #include<cstring> #defin ...
【noip 2009】乌龟棋记忆化搜索&动规
题目背景小明过生日的时候,爸爸送给他一副乌龟棋当作礼物. 题目描述乌龟棋的棋盘是一行N个格子,每个格子上一个分数(非负整数).棋盘第1格是唯一的起点,第N格是终点,游戏要求玩家控制一个乌龟棋子从起 ...

随机推荐

web项目的创建
1) 创建Mave的webapp项目 2) 在Pom文件中添加servlet-api的依赖 <dependency> <groupId>javax.servlet</gr ...
Maven学习总结（30）——Maven项目通用三级版本号说明
项目版本号说明当前版本号:1.0.0-SNAPSHOT 本项目采用通用的三级版本号,版本号格式是[主版本号].[副版本号].[修复版本号]-[稳定状态],如:1.0.0-SNAPS ...
MongoDB 数据文件备份与恢复
备份与恢复数据对于管理任何数据存储系统来说都是非常重要的. 1.冷备份与恢复——创建数据文件的副本(前提是要停止MongoDB服务器),也就是直接copy MongoDB将所有数据都存储在数据目录下, ...
洛谷—— P2149 [SDOI2009]Elaxia的路线
https://www.luogu.org/problem/show?pid=2149 题目描述最近,Elaxia和w的关系特别好,他们很想整天在一起,但是大学的学习太紧张了,他们必须合理地安排两 ...
定义SAP Portal Url别名
Defining URL Aliases Use A URL alias is the part of the portal URL after the section that specifies ...
配置类Configuration怎样使用
public class CorsConfiguration { /** * Wildcard representing <em>all</em> origins, metho ...
Android时间轴效果，直接使用在你的项目中
近期开发app搞到历史查询,受腾讯qq的启示,搞一个具有时间轴效果的ui,看上去还能够,然后立即想到分享给小伙伴,,大家一起来看看,先上效果图吧 watermark/2/text/aHR0cDovL2 ...
LeetCode 706. Design HashMap (设计哈希映射)
题目标签:HashMap 题目让我们设计一个 hashmap, 有put, get, remove 功能. 建立一个 int array, index 是key, 值是 value,具体看code. ...
【转】webview的几个问题
我们在native与网页相结合开发的过程中,难免会遇到关于WebView一些共通的问题.就我目前开发过程中遇到的问题以及最后得到的优化方案都将在这里列举出来.有些是老生常谈,有些则是个人摸索得出解决方 ...

[ NOIP 2009 ] TG

\(\#A\) \(Spy\)

\(\#B\) \(Son\)

\(\#C\) \(Trade\)

最短路：

\(Tarjan+DFS\)：

\(\#D\) \(Sudoku\)

\(DFS:\)

\(Dancing\ Links\ X:\)

[ NOIP 2009 ] TG的更多相关文章

随机推荐

热门专题