Restoring Numbers

　　

                                                                              D. Restoring Numbers

 

Vasya had two arrays consisting of non-negative integers: a of size n and b of size m. Vasya chose a positive integerk and created an n × m matrix v using the following formula:

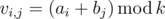
Vasya wrote down matrix v on a piece of paper and put it in the table.

A year later Vasya was cleaning his table when he found a piece of paper containing an n × m matrix w. He remembered making a matrix one day by the rules given above but he was not sure if he had found the paper with the matrix v from those days. Your task is to find out if the matrix w that you've found could have been obtained by following these rules and if it could, then for what numbers k, a1, a2, ..., an, b1, b2, ..., bm it is possible.

Input

The first line contains integers n and m (1 ≤ n, m ≤ 100), separated by a space — the number of rows and columns in the found matrix, respectively.

The i-th of the following lines contains numbers wi, 1, wi, 2, ..., wi, m (0 ≤ wi, j ≤ 109), separated by spaces — the elements of the i-th row of matrix w.

Output

If the matrix w could not have been obtained in the manner described above, print "NO" (without quotes) in the single line of output.

Otherwise, print four lines.

In the first line print "YES" (without quotes).

In the second line print an integer k (1 ≤ k ≤ 1018). Note that each element of table w should be in range between 0and k - 1 inclusively.

In the third line print n integers a1, a2, ..., an (0 ≤ ai ≤ 1018), separated by spaces.

In the fourth line print m integers b1, b2, ..., bm (0 ≤ bi ≤ 1018), separated by spaces.

有 a 数列 长度为n b 数列长度为m 都是非负整数， 然后 他们两个数组组成一个n*m的矩阵，然后 w[i][j]=(a[i]+b[j])%m;

最后给出了这个矩阵和n 和m 就数列 a 和 数列 b 还有m ， 令 a[0]-p=0;

那么我们得到了一个数列 0,a[2]-p-x1k...a[n]-xnk-p-  ; b[1]+p-y1k...b[n]+p- yn k, 然后

再搞出一个矩阵 m[i][j] 然后在abs（a[i]+b[i]-w[i][j]）=m[i][j] ;  当m中的每个元素都为0时 就可以知道w 中最大的那个+1就是答案了，还有就是有不为0的

可以将数列带进去看一下就发现 m[i][j]=x*k 这样求一次gcd就好了

#include <iostream>
#include <cstdio>
#include <string.h>
#include <stdlib.h>
using namespace std;
const int maxn=;
long long ma[maxn][maxn];
long long a[maxn],b[maxn];
long long e[maxn][maxn];
long long gcd(long long a, long long b){
    if(b==) return a;
    else return gcd(b,a%b);
}
int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)==){
           for(int i=; i<n; ++i)
             for(int j=; j<m;  ++j)
              scanf("%I64d",&ma[i][j]);
           a[]=;
           long long K;
           for(int i=; i<n; ++i)
             a[i]=ma[i][]-ma[][];
           for(int i=; i<m; ++i)
             b[i]=ma[][i];
           for(int i=; i<n; ++i)
             for(int j=; j<m ; ++j)
               e[i][j]=abs(a[i]+b[j]-ma[i][j]);
           bool falg=false;
           for(int i=; i<n; ++i)
             for(int j=; j<m; ++j)
              if(e[i][j]!=) falg=true;
           K=;
           if(falg==false){
              for(int i=; i<n; ++i)
                 for(int j=; j<m; ++j)
                  K=max(K,ma[i][j]);
                  K++;
                  puts("YES");
              printf("%I64d\n",K);
              for(int i=; i<n; ++i)
                 printf("%I64d%c",(a[i]%K+K)%K,i==n-?'\n':' ');

              for(int i=; i<m; ++i)
                 printf("%I64d%c",(b[i]%K+K)%K,i==m-?'\n':' ');

           }else{
               K=;
               bool finde=false;
              for(int i=; i<n; ++i){
                 if(finde) break;
               for(int j=; j<m; ++j){
                   if(e[i][j]!=){
                        K=e[i][j];
                     finde=true ; break;
                   }
               }
              }
              for(int i=; i<n; ++i)
              for(int j= ; j<m; ++j){
                  K=gcd(K,e[i][j]);
              }
              finde=true;
              for(int i=; i<n; ++i)
                 for(int j=; j<m; ++j)
                  if(ma[i][j]>=K) finde=false;
              if(finde==false){
                 puts("NO"); continue;
              }
                  puts("YES");
              printf("%I64d\n",K);
              for(int i=; i<n; ++i)
                 printf("%I64d%c",(a[i]%K+K)%K,i==n-?'\n':' ');
              for(int i=; i<m; ++i)
                 printf("%I64d%c",(b[i]%K+K)%K,i==m-?'\n':' ');
           }

    }
    return ;
}